Contextual levels
1. Introduction
Linguistics strives for a concise image of semantic (lexical) units and their arrangements in texts. The theory of networks and graphs offers some ways to solve this problem, see, e.g., (Watts 1999).
Many solutions of this problem have been achieved; one can find them in linguistic handbooks. We refer especially to the recent theoretical work by Ziegler & Altmann (2002: 85 ff.). The simplest presentation of the arrangements of the units is contained in binary relationships between all pairs of the units indicating presence or absence of a given relationship.
In Menzerath-Altmann’s text model based on a specific power law operating with the concepts of language construct and constituent, two contextual levels relevant for lexical units are defined and their connection proved in many texts. Segment is a part of a text of syntactic (sentence or clause), prosodic (verse) or some other quality chosen for the purpose of text analysis.
When a given lexical unit occurs in a segment, this segment functions as a constituent of a construct of all its constituents. According to Menzerath-Altmann’s law, the larger the construct, the shorter the mean size of its constituents. The contextual level of constituents is the level of segments. The contextual level of each construct is the level of the whole text. The two levels are mutually related in a way prescribed by the law. The relationships of lexical units at the level of segments can be described by means of a 1-0 symmetric matrix, in which lexical units are arranged as heads of both rows and columns. If a lexical unit is collocated with another unit in a text segment, the value of the respective entry of the matrix equals 1; if not, the entry equals 0. The matrix thus describes the contextual properties of segments. The question arises how the transition to the higher contextual level can be obtained.
2. Hypothesis
The assumed 1-0 symmetric matrix is an adjacency matrix to a graph depicting the semantic structure of the respective text. The following hypothesis can be applied for the purpose of describing the larger contextual relationships:
A higher level of contextuality of a text can be obtained from a 1-0 symmetric adjacency matrix as a matrix of the lengths of the shortest paths.
3. Derivation
Let us assume a matrix of values ai, j that depicts unoriented connections between a pair of vertices i, j 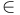 V = {1, 2, ..., i, ..., j, ..., v}. This matrix is an adjacency matrix G = (V, E) with
V = {1, 2, ..., i, ..., j, ..., v}. This matrix is an adjacency matrix G = (V, E) with 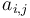 = 1 if i and j are connected with an unoriented edge (an element of the set E), and
= 1 if i and j are connected with an unoriented edge (an element of the set E), and 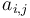 = 0 if there is no such connection between them.
= 0 if there is no such connection between them.
Consequently, the number of vertices in G is v and the number of edges equals 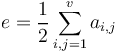 . G is a symmetric matrix with
. G is a symmetric matrix with 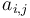 = 0 which means that no loops are present in the respective graph. This is the consequence of the fact that the presence or absence of each lexical unit in a segment is represented by the respective value 0 or 1 and nothing else. The following example illustrates how to operate with such matrices.
= 0 which means that no loops are present in the respective graph. This is the consequence of the fact that the presence or absence of each lexical unit in a segment is represented by the respective value 0 or 1 and nothing else. The following example illustrates how to operate with such matrices.
Example
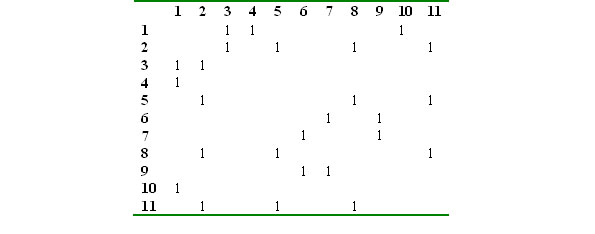
Let us assume matrix G as an adjacency matrix (zeros are omitted):
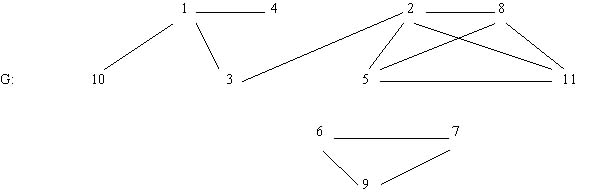
The respective graph to this matrix is presented in Figure 1.
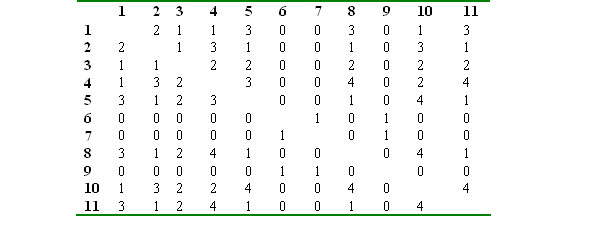
Let us further assume a matrix 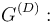
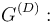
The relationship of matrices G and 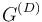 is described in the following points:
is described in the following points:
1.Both matrices are symmetric and have the same set of vertices V.
2.The values 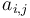 = 1, i ≠ j, of G are situated at the same (i, j) entries in
= 1, i ≠ j, of G are situated at the same (i, j) entries in 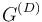 .
.
3.If in G there is 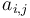 = 0, and at the same time it holds that
= 0, and at the same time it holds that 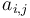 =k = 1 and
=k = 1 and 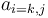 = 1, then
= 1, then 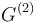 is obtained with
is obtained with 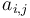 = 2; if not,
= 2; if not, 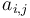 = 0 in
= 0 in 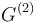 . The matrix
. The matrix 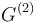 is the second step to
is the second step to 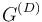 or it itself is
or it itself is 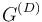 with D = 2. If in
with D = 2. If in 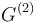 there remains
there remains 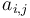 = 0 and at the same time
= 0 and at the same time 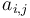 = k = 1 and
= k = 1 and 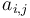 = k, j = 2, then in
= k, j = 2, then in 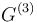
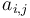 = 3.
= 3.
4.The process described at point 3 is repeated as many times as possible, resulting in the final 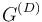 . At each step c, c = 1, 2,...,D, the newly changed entries of
. At each step c, c = 1, 2,...,D, the newly changed entries of 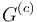 are set equal to c.
are set equal to c.
In the case of a matrix G more complex than in our example, finding the shortest paths for all pairs of vertices should be entrusted to a computer program. The standard algorithms for shortest paths are discussed in (Corman et al. 1990). Brandes (2001) presents the problem of shortest paths in the frame of the betweenness centrality in networks.
The obtained matrix 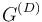 is completely derived from G. It indicates the distances between each pair of vertices as the length of the shortest path between the respective vertices. Its length is measured in the number of edges contained in a path. This is valid for each value
is completely derived from G. It indicates the distances between each pair of vertices as the length of the shortest path between the respective vertices. Its length is measured in the number of edges contained in a path. This is valid for each value 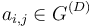 . The value of D can be understood as an expression of a semantic depth of a text. Many other semantic characteristics of a text can be obtained from the matrices.
(The above quoted example presents the semantic nucleus of a Chagatay poem written by Šıbānī, see (Eckmann 1966:268). Semantic nucleus of a text is defined by the set of vertices representing lexical units with frequencies higher than 1.)
. The value of D can be understood as an expression of a semantic depth of a text. Many other semantic characteristics of a text can be obtained from the matrices.
(The above quoted example presents the semantic nucleus of a Chagatay poem written by Šıbānī, see (Eckmann 1966:268). Semantic nucleus of a text is defined by the set of vertices representing lexical units with frequencies higher than 1.)
4. Author: L. Hřebíček.
5. References:
Brandes, U. (2001). A faster algorithm for betweenness centrality. Journal of Mathematical Sociology 25(2): 163-177.
Corman, T. H., Leiserson, C. E., and Rivest, R. L. (1990). Introduction to algorithms. MIT Press.
Eckmann, J. (1966). Chagatay manual. Mouton, The Hague.
Watts, D. J. (1999). Small worlds. The dynamics of networks between order and randomness. Princeton UP, Princeton (N. J.).
Ziegler, A., Altmann, G. (2002). Denotative Textanalyse. Ein textlinguistisches Arbeitsbuch. Edition Praesens, Wien.