Phoneme entropy and inventory
1. Problem and history
Entropy is a measure of disorder of the phoneme system or rather a measure of deviation from the uniformity of phoneme frequencies. If 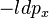 is the measure of self-information of a phoneme (px is the relative frequency of phoneme x) then
is the measure of self-information of a phoneme (px is the relative frequency of phoneme x) then
(1)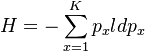
is the measure of average uncertainty or entropy. For different types of entropy see Naranan, Balasubrahmanyan (2000). Since px is estimated as fx/N (N being the sample size), (1) can be written as
(2)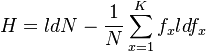
Since ranked frequencies of phonemes ( ) abide by a specific distribution, there is the justified question whether H depends on the size of the inventory of phonemes K.
Altmann and Lehfeldt (1980) used the model of the 1-displaced right truncated geometric distribution to show that entropy depends on K, Zörnig and Altmann (1983, 1984) used the Zipf-Mandelbrot distribution to derive another formula.
Cohen, Mantegna and Havlin (1997) observed a parabolic curve for the dependence between word inventory and entropy.
) abide by a specific distribution, there is the justified question whether H depends on the size of the inventory of phonemes K.
Altmann and Lehfeldt (1980) used the model of the 1-displaced right truncated geometric distribution to show that entropy depends on K, Zörnig and Altmann (1983, 1984) used the Zipf-Mandelbrot distribution to derive another formula.
Cohen, Mantegna and Havlin (1997) observed a parabolic curve for the dependence between word inventory and entropy.
2. Hypothesis
The entropy depends on the size of the phoneme inventory.
3. Derivation
3.1. From the geometric distribution (Altmann, Lehfeldt 1980)
Let the ranked frequencies of phonemes ( ) follow the 1-displaced right truncated geometric distribution defined as
) follow the 1-displaced right truncated geometric distribution defined as
(3)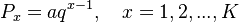
with
(3)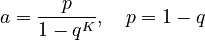
then (1) can be written as
(4)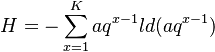 .
.
Summing and using (3) one obtains
(5)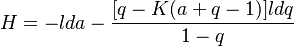 .
.
Since a + q -1 ≈ 0 and 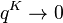 for great K, (5) results in
for great K, (5) results in
(6)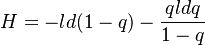 .
.
Substituting 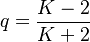 as the first approximation (see also Phonemes: Repeat rate)
as the first approximation (see also Phonemes: Repeat rate)
one obtains
(7)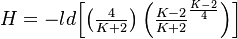 .
.
(Example: see below)
3.2. From the Zipf-Mandelbrot distribution (Zörnig, Altmann 1984)
Let the ranked frequencies be distributed according to
(8)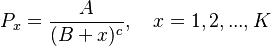
where c = 1 brought already a good approximation in case of Repeat rate ( ), we consider
), we consider
(9)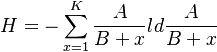 ,
,
A being the normalizing constant, i.e.
(10)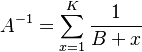 .
.
Since ld x = (ld e)(ln x) we obtain from (9)
(11)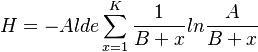
= 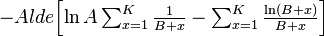 .
.
Inserting (10) in (11) yields
(12)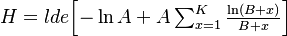 .
.
Approximating A by an appropriate integral, we obtain
(13)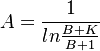 .
.
and in the same way
(14)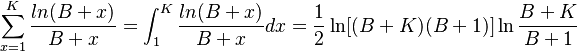 .
.
Inserting (13) and (14) in (12) and ordering one obtains at last
(15)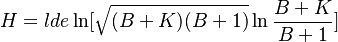 .
.
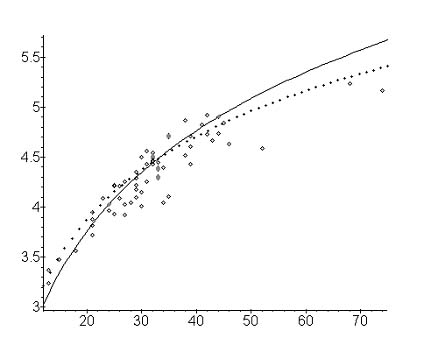
Example. Entropy of phoneme systems for 63 languages.
Altmann, Lehfeldt (1980) and Zörnig, Altmann (1984) fitted the above curves (7) and (15) to the empirical entropies in 63 languages and obtained the results shown in Table 1. Zörnig and Rothe (1990) added further 8 data from French and German. The best value of B was iteratively established at B = 0.61 and B = 0.27. However, B is not yet interpreted. The languages are the same as in the tables in Repeat rate ( ). Here the coefficient of determination has been ascertained in such a way that the values of H for the same K were averaged.
). Here the coefficient of determination has been ascertained in such a way that the values of H for the same K were averaged.
Evidently, the fitting is slightly better using Zipf-Mandelbrot´s distribution. Again, even if the fitting is satisfactory, further research must be done.
Note. Using the geometric distribution for the derivation of Repeat rate (R) and Entropy (H) the following relationship between them follows
(16)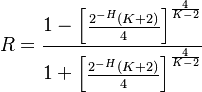
and
(17)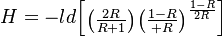 .
.
Using the Zipf-Mandebrot distribution we obtain
(18)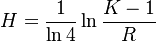 and
and
(19)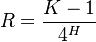 .
.
so that it is sufficient to compute one of these values.
4. Authors: G. Altmann.
5. References (contains also references in which merely entropy has been computed)
Altmann, G., Bagheri, D., Goebl, H., Köhler, R., Prün, C. (2002). Einführung in die quantitative Lexikologie. Götingen: Peust & Gutschmidt.
Altmann, G., Lehfeldt, W. (1980). Einführung in die quantitative Phonologie. Buchum: Brockmeyer.
Cohen, A., Mantegna, R.N., Havlin, S. (1997). Numerical analysis of word frequencies in artificial and natural language texts? Fractals 5(1), 93-104.
Feng, Zh. (1984). Hanzi de shang (Entropy of Chinese characters). In: Wenzi gaige 4, ….[Reprint in Chen, Y. (1989)(ed.), Xiandai Hanyu dingliang fenxi: 267-278 (Quantitative analysis of modern Chinese). Shanghai: Shanghai Jiaoyu chubanse.
Jakopin, F. (2002). Entropija v slovenskih leposlovnih besedilih. Ljubljana: ZRC SAZU.
Kučera, K. (2001). The development of entropy and redundancy in Czech from the 13th to the 20th century: Is there a linguistic arrow of time. In: Uhlířova, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a linguistic paradigm: levels, constituents, constructs. Festschrift in honour of Ludek Hřebíček: 153-162. Trier: WVT.
Lin, L. (2001). Guabyu Hanzi tongji tezheng de ji ge wenti. In: Su, P. (ed.), Hiandai Hanzixue cankao ziliao:….. (Reference data to modern sinographics.) Peking: beijing Daxue chubanshe.
Lua, K.T. (1994). Frequency-rank curves and entropy for Chinese characters and words. Computer Processing of Chinese and Oriental Languages 8,(1), 37-52.
Naranan, S., Balasubrahmanyan, V.K. (2000). Information theory and algorithmic complexity: Applications to linguistic discourses and DNA sequences as complex systems. Part I: Efficiency of the genetic code of DNA. J. of Quantitative Linguistics 7, 129-151; Part II: Conmplexity of DNA sequences, analogy with linguistic discourses. J. of Quantitative Linguistics 7, 153-183.
Rothe, U., Zörnig, P. (1989). The entropy of phoneme frequencies. German and French. Glottometrika 11, 199-205.
Yannakoudakis, E.J., Tsomokos, I., Hutton, P.J. (1990). n-Grams and their implication to natural language understanding. Pattern Recognition 23,(5), 509-528.
Zörnig, P., Altmann, G. (1983). The repeat rate of phoneme frequencies and the Zipf-Mandelbrot law. Glottometrika 5, 205-211.
Zörnig, P., Altmann, G. (1984). The entropy of phoneme frequencies and the Zipf-Mandelbrot law. Glottometrika 6, 41-47.