Difference between revisions of "Polysemy and age"
m |
|||
| Line 16: | Line 16: | ||
where x is the time interval and y is the polysemy. The solution is | where x is the time interval and y is the polysemy. The solution is | ||
| − | (2)<math> y= ax^b e^{bx}\quad</math> | + | (2)<math> y= ax^b e^{bx}\quad</math> |
where <math>a = e^C</math>, C being the integration constant. The curve goes to infinity but Wolff found even words with 95 meanings. There is surely a finite limit being in agreement with the principles of synergetic linguistics but it cannot preliminarily be deduced. | where <math>a = e^C</math>, C being the integration constant. The curve goes to infinity but Wolff found even words with 95 meanings. There is surely a finite limit being in agreement with the principles of synergetic linguistics but it cannot preliminarily be deduced. | ||
Latest revision as of 13:03, 26 January 2012
1. Problem and history
The longer a word exists the more meanings it can acquire. It does not hold generally for any word but it holds on the average for ensembles of words that came into existence in the same time interval. The greatest problem is that even if one has a historical dictionary, the time of birth is merely approximate, since dictionaries vonsider the first appearing in texts. The first count has been performed by Wollf (1972) who counted the present number of meanings of English words that appeared in different centuries and periods of the evolution of English. The fate of particular Japanese words has been considered by Sanada (1999) but there are merely graphs, no numbers. A theoretical approach has been made by Strauss and Altmann (2003) which is in agreement with the “unified derivation” proposed by Wimmer and Altmann (2005).
2. Hypothesis
The older an ensemble of words coming into existence in the same time interval, the more meanings have the words on the average.
3. Derivation
The relative rate of polysemy increase is proportional to the relative rate of time interval change. Since words are not differentiated according to frequency, length, polytexty etc. all these factors are considered a constant ceteris paribus condition. In the simplest case the proportionality factor and the ceteris paribus constant are equal, yielding the equation
(1)
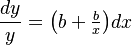
where x is the time interval and y is the polysemy. The solution is
(2)
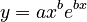
where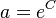 
, C being the integration constant. The curve goes to infinity but Wolff found even words with 95 meanings. There is surely a finite limit being in agreement with the principles of synergetic linguistics but it cannot preliminarily be deduced.
Example: Age and polysemy in English
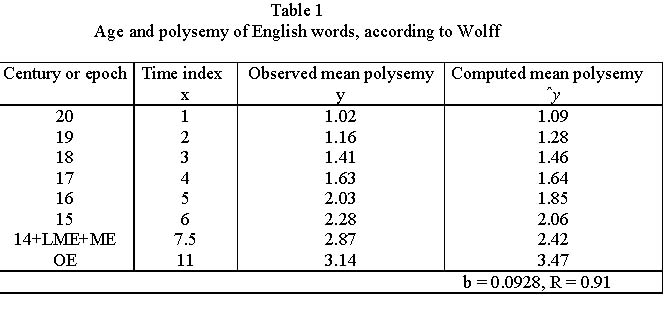
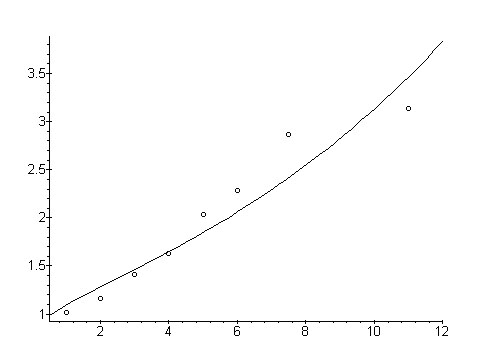
Wolff (1972) considered the age of English words and their polysemy, unfortunately truncating the polysemy above 10. Strauss and Altmann (2003) computed the mean polysemy for individual time intervals and fitted (2) to the data. The results are presented in Table 1, where the time index shows the time depth. The constant a ≈ 1. The graphical representation can bee seen in Fig. 1.
4. Authors: U. Strauss, G. Altmann
5. References
Sanada, H. (1999). Analysis of Japanese vocabulary by the theory of synergetic linguistics. J. of Quantitative Linguistics 6, 239-251.
Strauss, U., Altmann, G. (2003). Age and polysemy of words. Glottometrics 6, 61-64.
Wimmer, G., Altmann, G. (2005). Unified derivation of some linguistic laws. In: Peter Grzybek (ed.), Contributions to the Science of Language. Word Length Studies and Related Issues (in print). Dordrecht, NL: Kluwer.
Wolff, D. (1972). Bedeutungshäufigkeit und ihr statistisches Verhalten. Beiträge zur Linguistik und Informationsverarbeitung 22, 33-44.
