Difference between revisions of "Frequency and polytextuality"
m (Frequency and polytexty moved to Frequency and polytextuality) |
|||
| (19 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
'''1. Problem and history''' | '''1. Problem and history''' | ||
| − | + | Polytextuality measures the degree of independence of the usability of a word (in general of a linguistic unit) of its co-text or context. Linguistic units such as phonemes, syllables, morae, morphemes, words etc. differ in their usability with respect to different environments. The environment of a syllable, mora or morphem consists of the words in which they occur, the environment of a word consists of phrases, sentences, or texts. The number of different environments is often called the number of types. The frequency of a given entity in all its environments in, say, a corpus, is considered as the number of tokens. It can be shown that there exists a lawful relationship between the number of types (environments) and the number of tokens (frequency) of units on the given level. | |
| + | The degree of independence of the unsability of a unit from its context (or, the variability of contextes with respect to a given unit), can be measured in several ways. Word polytextuality is often measured in terms of the number of different texts in a text corpus which contain at least one token of the given word. Polytextuality of morphemes or syllables are usually measured with reference to an inventory such as a dictionary. | ||
| − | The relationship between frequency and polytextuality has been | + | The relationship between frequency and polytextuality has been postulated and investigated by R. Köhler (1986) as a complement to other quantitative properties, in order to integrate it into his synergetic control cycle. As a consequence of an erroneous identification with another “type-token” problem (<math>\rightarrow</math>), one can find this relationship also under the name “(morphological) productivity” (cf. Baayen 2001), which in turn represents a slightly different aspect (cf. Wimmer, Altmann 1995). The relationship was studied in different works on language synergetics (cf. e.g. Gieseking 2002), Köhler (2005) reformulated the pertinent part of his control cycle and Tamaoka, Altmann (2005) showed by means of Japanese morae that the unified theory (<math>\rightarrow</math>) leads to an identical result. |
Usually one considers frequency as the spiritus movens, the independent variable of many relationships, but Köhler (1986) assumed here an inverse relationship. | Usually one considers frequency as the spiritus movens, the independent variable of many relationships, but Köhler (1986) assumed here an inverse relationship. | ||
| Line 13: | Line 14: | ||
'''3. Derivation''' | '''3. Derivation''' | ||
| − | Since in most cases linguistic properties are related by their relative rates of change, Tamaoka | + | Since in most cases linguistic properties are related by their relative rates of change, Tamaoka (2007), taking into account some ceteris paribus factors, and leaning against the unified theory (<math>\rightarrow</math>) set up the equation |
| − | (1)<math> \frac{dy}{y}= \left( c+\frac{b}{x}\right)dx</math> | + | (1) <math> \frac{dy}{y}= \left( c+\frac{b}{x}\right)dx</math> |
| − | where x is polytexty, y is frequency and c | + | where x is polytexty, y is frequency and c represents some additional factors. The resulting solution, |
| − | (2)<math>y = ax^b e^{cx}\quad</math>. | + | (2) <math>y = ax^b e^{cx}\quad</math>, |
| + | |||
| + | was used to model polytexty and frequency of Japanese morae in a Japanese corpus. | ||
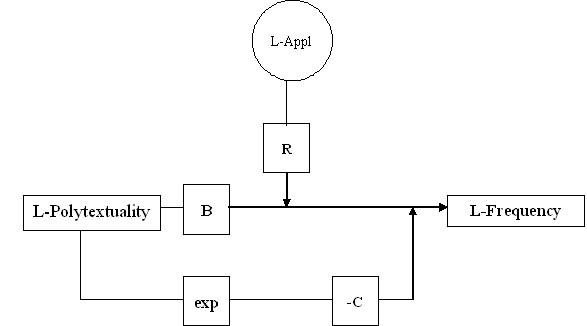
Using Köhlers model (Fig. 1) one can write the relationships as follows: | Using Köhlers model (Fig. 1) one can write the relationships as follows: | ||
| − | (3) ln(F) = R ln(Appl) + B ln(PT) – C exp(ln(PT)) | + | (3) ln(F) = R ln(Appl) + B ln(PT) – C exp(ln(PT)) |
i.e. | i.e. | ||
| − | |||
| − | from which | + | ln(F) = R ln(Appl) + B ln(PT) – C (PT) |
| + | |||
| + | from which it follows that | ||
| + | |||
| + | <math>F = Appl^R PT^B e^{-c({PT})}\quad</math>. | ||
| − | <math> | + | Since in the framework of a synchronic study <math>Appl^R</math> can be considered as a constant, say A, and since we can set PT = x and F = y, we obtain |
| − | + | <math>y = A x^b e^{-cx}\quad</math>, | |
| − | + | whih is identical with the above solution of the differential equation. | |
| − | + | <div align="center">[[Image:Figur1_Freq.jpg]]</div> | |
| + | <div align="center">Fig. 1. The relationship between polytextuality and frequency in general</div> | ||
| − | |||
| − | |||
Thus Köhler´s model explains also the additional factors. | Thus Köhler´s model explains also the additional factors. | ||
| − | '''Example 1'''. Types and | + | '''Example 1'''. Types and tokens of Japanese morae |
Tamaoka and Makioka (2004) computed the frequencies of 103 Japanese morae in a corpus containing 341,771 different words with total frequency 287,792,797. For each mora its frequency and the contexts (different words) were ascertained. Tamaoka and Altmann (2005) showed that the best fit to these data (in logarithmic transformation) can be obtained by the curve | Tamaoka and Makioka (2004) computed the frequencies of 103 Japanese morae in a corpus containing 341,771 different words with total frequency 287,792,797. For each mora its frequency and the contexts (different words) were ascertained. Tamaoka and Altmann (2005) showed that the best fit to these data (in logarithmic transformation) can be obtained by the curve | ||
| Line 51: | Line 56: | ||
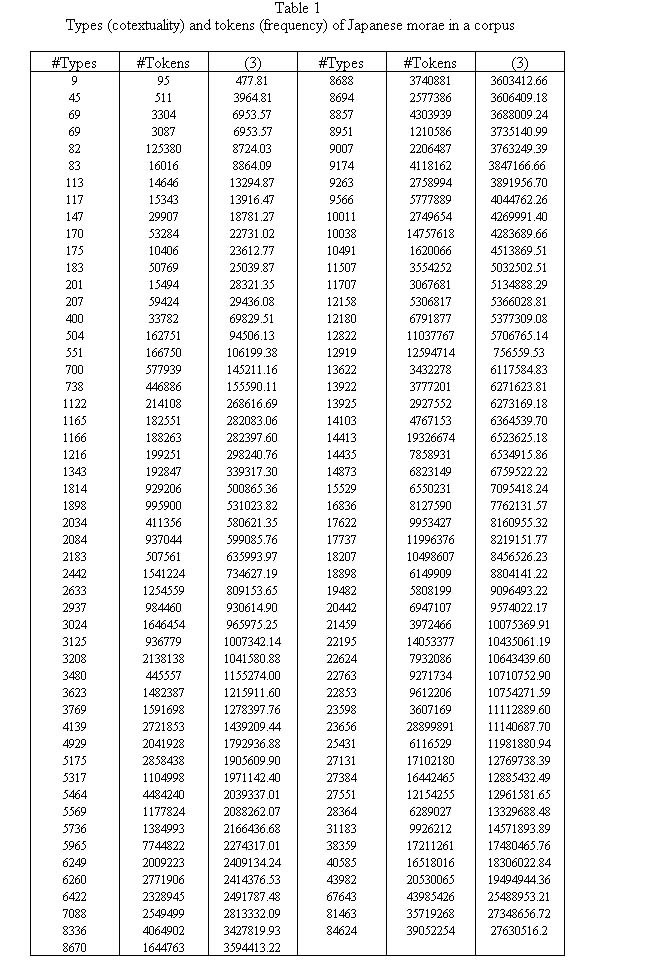
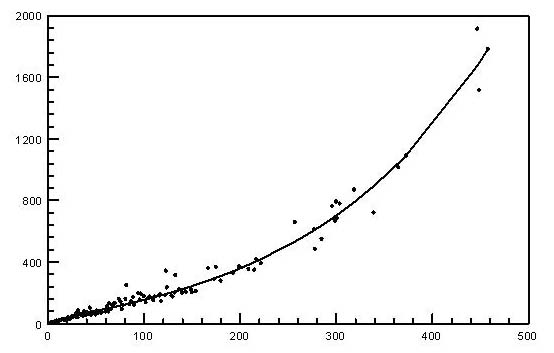
yielding a determination coeffciient D = 0.92. The result of fitting is displayd in Table 1 and graphically presented in Fig. 2. | yielding a determination coeffciient D = 0.92. The result of fitting is displayd in Table 1 and graphically presented in Fig. 2. | ||
| − | <div align="center">[[Image: | + | <div align="center">[[Image:Tabelle11_Freq.jpg]]</div> |
<div align="center">[[Image:Grafi1_Freq.jpg]]</div> | <div align="center">[[Image:Grafi1_Freq.jpg]]</div> | ||
| − | <div align="center">Fig. 2. Relation between types and tokens of Japanese morae</div> | + | <div align="center">Fig. 2. Relation between types and tokens of Japanese morae</div> |
| + | |||
| + | '''Example 2'''. Polytextuality of German words as a function of their frequencies | ||
| + | |||
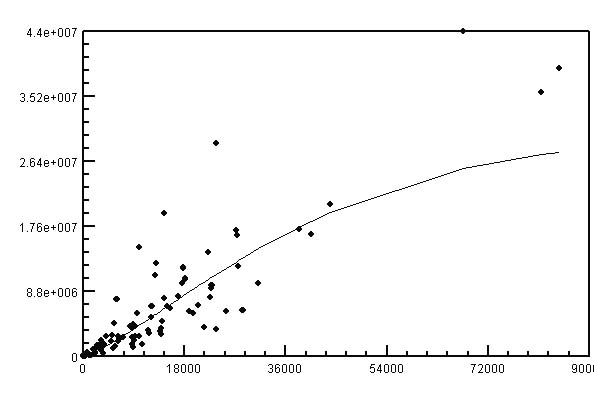
| + | Köhler (1986) published his result on data of a German text corpus (LIMAS), respresented here by the following graph: | ||
| + | |||
| + | [[image:Graph1.JPG]] | ||
| + | |||
| − | '''4. Authors: R. Köhler | + | '''4. Authors: G. Altmann, R. Köhler''' |
| Line 65: | Line 77: | ||
'''Gieseking, K.''' (2002). Untersuchungen zur Synergetik der englischen Lexik. In: Köhler, R. (ed.), ''Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 387-433''. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/ | '''Gieseking, K.''' (2002). Untersuchungen zur Synergetik der englischen Lexik. In: Köhler, R. (ed.), ''Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 387-433''. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/ | ||
| − | '''Köhler ( | + | '''Köhler, R.''' (2006). Frequenz, Kontextualität und Länge von Wörtern. Eine Erweiterung des synergetisch-linguistischen Modells. In: Rapp, R., Sedlmeier, P., Zunker-Rapp, G. (eds.), ''Perspectives on Cognition''. Lengerich, Berlin, Bremen, Miami et al: Pabst Science Publishers, 327-338. |
| − | '''Tamaoka, K | + | '''Tamaoka, K.''' (2007). On the relation between types and tokens of Japanese morae. In: ''Script problems (in print)''. |
'''Tamaoka, K., Makioka, Sh.''' (2004). Frequency of occurrence for units of phonemes, morae, and syllables appearing in a lexical corpus of a Japanese newspaper. ''Behavior Research Methods, Instruments & Computers 36(3), 531-547''. | '''Tamaoka, K., Makioka, Sh.''' (2004). Frequency of occurrence for units of phonemes, morae, and syllables appearing in a lexical corpus of a Japanese newspaper. ''Behavior Research Methods, Instruments & Computers 36(3), 531-547''. | ||
| Line 73: | Line 85: | ||
'''Wimmer, G., Altmann, G.''' (1995). A model of morphological productivity. ''J. of Quantitative Linguistics 2, 212-216.'' | '''Wimmer, G., Altmann, G.''' (1995). A model of morphological productivity. ''J. of Quantitative Linguistics 2, 212-216.'' | ||
| − | [[Category: | + | [[Category:Quantitative properties]] |
Latest revision as of 13:13, 26 June 2007
1. Problem and history
Polytextuality measures the degree of independence of the usability of a word (in general of a linguistic unit) of its co-text or context. Linguistic units such as phonemes, syllables, morae, morphemes, words etc. differ in their usability with respect to different environments. The environment of a syllable, mora or morphem consists of the words in which they occur, the environment of a word consists of phrases, sentences, or texts. The number of different environments is often called the number of types. The frequency of a given entity in all its environments in, say, a corpus, is considered as the number of tokens. It can be shown that there exists a lawful relationship between the number of types (environments) and the number of tokens (frequency) of units on the given level. The degree of independence of the unsability of a unit from its context (or, the variability of contextes with respect to a given unit), can be measured in several ways. Word polytextuality is often measured in terms of the number of different texts in a text corpus which contain at least one token of the given word. Polytextuality of morphemes or syllables are usually measured with reference to an inventory such as a dictionary.
The relationship between frequency and polytextuality has been postulated and investigated by R. Köhler (1986) as a complement to other quantitative properties, in order to integrate it into his synergetic control cycle. As a consequence of an erroneous identification with another “type-token” problem ( ), one can find this relationship also under the name “(morphological) productivity” (cf. Baayen 2001), which in turn represents a slightly different aspect (cf. Wimmer, Altmann 1995). The relationship was studied in different works on language synergetics (cf. e.g. Gieseking 2002), Köhler (2005) reformulated the pertinent part of his control cycle and Tamaoka, Altmann (2005) showed by means of Japanese morae that the unified theory (
), one can find this relationship also under the name “(morphological) productivity” (cf. Baayen 2001), which in turn represents a slightly different aspect (cf. Wimmer, Altmann 1995). The relationship was studied in different works on language synergetics (cf. e.g. Gieseking 2002), Köhler (2005) reformulated the pertinent part of his control cycle and Tamaoka, Altmann (2005) showed by means of Japanese morae that the unified theory ( ) leads to an identical result.
) leads to an identical result.
Usually one considers frequency as the spiritus movens, the independent variable of many relationships, but Köhler (1986) assumed here an inverse relationship.
2. Hypothesis
The frequency of linguistic units depends on their polytextuality.
3. Derivation
Since in most cases linguistic properties are related by their relative rates of change, Tamaoka (2007), taking into account some ceteris paribus factors, and leaning against the unified theory ( ) set up the equation
) set up the equation
(1) 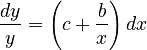
where x is polytexty, y is frequency and c represents some additional factors. The resulting solution,
(2) 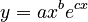 ,
,
was used to model polytexty and frequency of Japanese morae in a Japanese corpus.
Using Köhlers model (Fig. 1) one can write the relationships as follows:
(3) ln(F) = R ln(Appl) + B ln(PT) – C exp(ln(PT))
i.e.
ln(F) = R ln(Appl) + B ln(PT) – C (PT)
from which it follows that
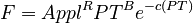 .
.
Since in the framework of a synchronic study 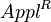 can be considered as a constant, say A, and since we can set PT = x and F = y, we obtain
can be considered as a constant, say A, and since we can set PT = x and F = y, we obtain
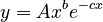 ,
,
whih is identical with the above solution of the differential equation.
Thus Köhler´s model explains also the additional factors.
Example 1. Types and tokens of Japanese morae
Tamaoka and Makioka (2004) computed the frequencies of 103 Japanese morae in a corpus containing 341,771 different words with total frequency 287,792,797. For each mora its frequency and the contexts (different words) were ascertained. Tamaoka and Altmann (2005) showed that the best fit to these data (in logarithmic transformation) can be obtained by the curve
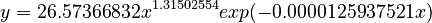 .
.
yielding a determination coeffciient D = 0.92. The result of fitting is displayd in Table 1 and graphically presented in Fig. 2.
Example 2. Polytextuality of German words as a function of their frequencies
Köhler (1986) published his result on data of a German text corpus (LIMAS), respresented here by the following graph:
4. Authors: G. Altmann, R. Köhler
5. References
Baayen, R.H. (2001). Word frequency distributions. Dordrecht: Kluwer.
Gieseking, K. (2002). Untersuchungen zur Synergetik der englischen Lexik. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 387-433. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/
Köhler, R. (2006). Frequenz, Kontextualität und Länge von Wörtern. Eine Erweiterung des synergetisch-linguistischen Modells. In: Rapp, R., Sedlmeier, P., Zunker-Rapp, G. (eds.), Perspectives on Cognition. Lengerich, Berlin, Bremen, Miami et al: Pabst Science Publishers, 327-338.
Tamaoka, K. (2007). On the relation between types and tokens of Japanese morae. In: Script problems (in print).
Tamaoka, K., Makioka, Sh. (2004). Frequency of occurrence for units of phonemes, morae, and syllables appearing in a lexical corpus of a Japanese newspaper. Behavior Research Methods, Instruments & Computers 36(3), 531-547.
Wimmer, G., Altmann, G. (1995). A model of morphological productivity. J. of Quantitative Linguistics 2, 212-216.