Difference between revisions of "Complexity of syntactic constructions"
RVulanovic (talk | contribs) m |
|||
| (2 intermediate revisions by one other user not shown) | |||
| Line 20: | Line 20: | ||
I(K) – the size of inventory of constructions. | I(K) – the size of inventory of constructions. | ||
| − | Assumptions: The number of constructions with complexity x+1 is proportional to that with complexity x. maxH increases the probability of a higher complexity, minX decreases it. E | + | Assumptions: The number of constructions with complexity x+1 is proportional to that with complexity x. maxH increases the probability of a higher complexity, minX decreases it. The greater E, the more complexity is needed to code the individual messages. On the other hand, the greater the inventory size I(K), the less complexity is needed. With these assumptions, we obtain |
| − | |||
(1)<math> P_{x+1}= \frac{maxH + x}{minX + x} \frac{E}{I(K)}P_x, \quad x= 1, 2, ...</math> | (1)<math> P_{x+1}= \frac{maxH + x}{minX + x} \frac{E}{I(K)}P_x, \quad x= 1, 2, ...</math> | ||
| − | Setting maxH = k-1, minX = m-1 | + | Within a given period of time, the relation E/I(K) can be considered as a constant, say q. Setting E/I(K) = q, maxH = k-1, and minX = m-1, from (1) we get |
(2)<math> P_{x+1} = \frac{k+x-1}{m+x-1}qP_x, \quad x=1, 2, ...</math> | (2)<math> P_{x+1} = \frac{k+x-1}{m+x-1}qP_x, \quad x=1, 2, ...</math> | ||
Latest revision as of 17:26, 11 December 2006
1. Problem and history
The complexity of a syntactic construct is measured in terms of the number of its immediate constituents. The partitioning in immediate constituents can be performed on the basis of any grammar. The first model seems to be that of Köhler and Altmann (2000).
2. Hypothesis
The complexity of syntactic constructions follows the hyper-Pascal distribution.
3. Derivation
The complexity depends on following quantities (Köhler, Altmann 2000:192):
minX – the requirement of minimization of the complexity of a syntactic construction in order to decrease memory effort in processing the construction;
maxH – the requirement of maximazing compactness. This enables us diminishing the complexity of the subordinated level of embedding by embedding constituents into the given level… minX on the level m corresponds to the requirement maxH on the level m+1;
E – a variable representing the average degree of fullness, the default value of complexity;
I(K) – the size of inventory of constructions.
Assumptions: The number of constructions with complexity x+1 is proportional to that with complexity x. maxH increases the probability of a higher complexity, minX decreases it. The greater E, the more complexity is needed to code the individual messages. On the other hand, the greater the inventory size I(K), the less complexity is needed. With these assumptions, we obtain
(1)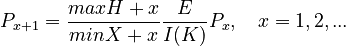
Within a given period of time, the relation E/I(K) can be considered as a constant, say q. Setting E/I(K) = q, maxH = k-1, and minX = m-1, from (1) we get
(2)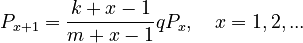
resulting in
(3)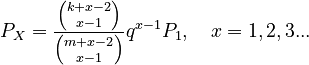
where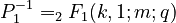 .
.
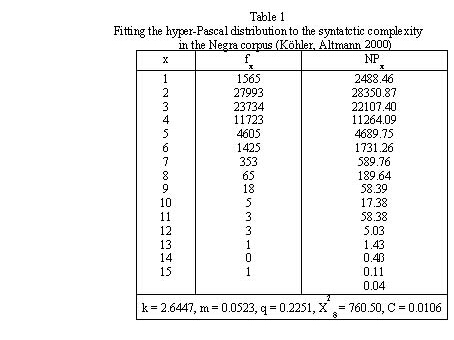
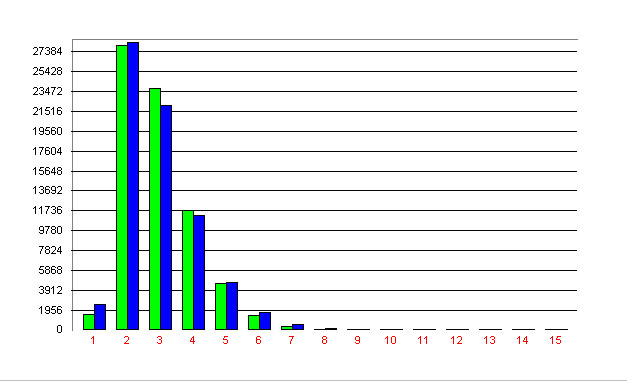
Example: Complexity of syntactic constructions in the Negra corpus (Brants 1999) Köhler and Altmann (2000) fitted (3) to the complexity of syntactic constructions in the Negra corpus. The result is presented in Table 1 and Fig. 1.
Since the number of observations is too great, the use of the chi-square is problematic. The authors use the contingency coefficient 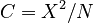 which is acceptable. It would be advisable to use single texts instead of corpora.
which is acceptable. It would be advisable to use single texts instead of corpora.
4. Authors: G. Altmann
5. References
Brants, T. (1999). Tagging and parsing with cascaded Markov models. Automation of corpus annotation. Saarbrücken: Universität der Saarlandes.
Köhler, R., Altmann, G. (2000). Probability distributions of syntactic units and properties. J. of Quantitative Linguistics 7, 189-200.