Difference between revisions of "Diversification"
m |
m |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
For the sake of illustration let us show some concrete examples: | For the sake of illustration let us show some concrete examples: | ||
| − | + | 1) The word can enlarge its class membership without any change, e.g. through conversion: “the hand”, “to hand”. | |
| − | + | 2) The stem enlarges its class membership through derivation, e.g. German "Bild", "bilden", "bildhaft", or vocalization in Semitic languages, etc. | |
| − | + | 3) The stem can enlarge its applicability within one class through derivation e.g. German "Blut", "Blutung", "Bluter", or through vocalization, etc. | |
| − | + | 4) The stem can enlarge its applicability within one class through compounding e.g. "Blut", "Blutdruck", "Blutdurst", etc. | |
| − | + | 5) If a language abandons isolating morphology, then morphemes diversify into several morphs because of agglutination or inflection (sequential or syntactic dependence). | |
| − | + | 6) The word can enlarge its applicability in the sentence by acquiring several functions, i.e. it enlarges its dispositional properties, which are different from the constant grammatical properties, e.g. practically every word can become the subject of a sentence. | |
| − | + | 7) Verbs can enlarge their valence, i.e. their combinability with different cases. | |
| − | + | 8) The word can enlarge its cotextuality (cf. Köhler 1986), i.e. its ability to occur in several contexts (where "context" can be defined in several ways). The reverse of this kind of diversification process is part of style formation, where a "position" diversifies, i.e., a position in a given context can be filled with different units (words, sentences, etc.). | |
| − | + | 9) A concept can be expressed by different forms, giving rise to dialects, sociolects, idiolects, or to synonymy. | |
| − | + | 10) A word can acquire different meaning (polysemy). | |
| − | + | 11) Every word can acquire different associations (connotations). | |
Diversified entities abide by a ranking law, i.e. if the members of the diversified entity are ordered according to their frequency, then the frequencies are “lawfully” connected. | Diversified entities abide by a ranking law, i.e. if the members of the diversified entity are ordered according to their frequency, then the frequencies are “lawfully” connected. | ||
| Line 31: | Line 31: | ||
The factors of diversification can be as follows (Altmann 2005): | The factors of diversification can be as follows (Altmann 2005): | ||
| − | + | a) ''Random fluctuation'' which is omnipresent in any language phenomena. | |
| − | + | b) ''Environmentally conditioned variation'' forcing an element to acquire different forms or meaning nuances in different environments. | |
| − | + | c) ''Conscious change'' through conscious creation, borrowing, emotionality etc. | |
| − | + | d) ''Self-organisatory triggering'' of a process to a limit, causing changes on other levels, too. | |
| − | + | e) ''System modification'' joined with local or global modifications in a subsystem, | |
| − | + | f) ''Köhlerian requirements'' (Köhler 1986, 1987, 1989, 1990, 1991) forcing to take into account collateral pressures form different sides. They are as follows: (i) ''The trend for minimal coding and deciding effort'', (ii) ''sufficient redundancy'', (iii) ''the coding requirement in general'', (iv) ''context economy vs. context specificity'', and (v) ''invariance vs. flexibility of relation between expression and meaning.'' | |
| − | The concepts of diversification and unification go back to G.K. Zipf (1935, 1949). Together they are called “Zipfian processes”. The scope of the phenomena is enormous. Semantic phenomena have been examined by Beöthy and Altmann (1984a,b, 1991), Altmann (1985a), Altmann, Best, Kind (1987); grammatical phenomena were analyzed in the omnibus volume edited by Rothe (1991), where also a study on spelling errors in | + | The concepts of diversification and unification go back to G.K. Zipf (1935, 1949). Together they are called “Zipfian processes”. The scope of the phenomena is enormous. Semantic phenomena have been examined by Beöthy and Altmann (1984a,b, 1991), Altmann (1985a), Altmann, Best, Kind (1987); grammatical phenomena were analyzed in the omnibus volume edited by Rothe (1991), where also a study on spelling errors in English can be found, and dialectal diversification was studied by Altmann (1985b). |
The laws hold usually for ranked nominal classes of limited size. | The laws hold usually for ranked nominal classes of limited size. | ||
| Line 78: | Line 78: | ||
(1) <math>P_x=g(x)P_{x-1}\quad</math>, where <math>g(x)\le 1\quad</math>. | (1) <math>P_x=g(x)P_{x-1}\quad</math>, where <math>g(x)\le 1\quad</math>. | ||
| − | Furthermore, g(x) can be written as | + | Furthermore, <math>g(x)</math> can be written as |
<math>g(x)=\frac{f(x)}{h(x)}</math>, | <math>g(x)=\frac{f(x)}{h(x)}</math>, | ||
| − | where f(x) is a function composed of a language constant a and the diversifying effect of the speaker bx, i.e. f(x) = a+bx, while h(x) contains the controlling, regulating effect of the hearer (community) cx, i.e. | + | where <math>f(x)</math> is a function composed of a language constant <math>a</math> and the diversifying effect of the speaker <math>bx</math>, i.e. <math>f(x) = a+bx</math>, while <math>h(x)</math> contains the controlling, regulating effect of the hearer (community) <math>cx</math>, i.e. |
| − | <math>g(x)=\frac{a+bx}{cx} | + | <math>g(x)=\frac{a+bx}{cx} \le 1</math>, (a, b, and c are assumed positive), |
so that | so that | ||
| − | (2)<math>P_x=\frac{a+bx}{cx} | + | (2) <math>P_x=\frac{a+bx}{cx}P_{x-1}</math>. |
| − | In order to obtain a known distribution, one can reparametrize (2) by writing a/b = k-1 and b/c = q, and solving (2) for | + | In order to obtain a known distribution, one can reparametrize (2) by writing <math>a/b = k-1</math> and <math>b/c = q</math>, and solving (2) for <math>P_x</math>. One obtains |
| − | (3)<math>P_x=\begin{pmatrix}k&+&x&-&1\\&&x\end{pmatrix}\frac{p^kq^x}{1-p^k}, \quad x=1,2,3,...</math> | + | (3) <math>P_x=\begin{pmatrix}k&+&x&-&1\\&&x\end{pmatrix}\frac{p^kq^x}{1-p^k}, \quad x=1,2,3,...</math> |
yielding the zero-truncated (positive) negative binomial distribution. The condition <math>g(x)\le 1</math> is fulfilled if <math>kq\le 1</math>. | yielding the zero-truncated (positive) negative binomial distribution. The condition <math>g(x)\le 1</math> is fulfilled if <math>kq\le 1</math>. | ||
| Line 102: | Line 102: | ||
For the purposes of dialectal variation captured in terms of numbers of lexeme variants on maps of a dialect atlas, Altmann (1985) used the birth-and-death process based on the following assumptions: | For the purposes of dialectal variation captured in terms of numbers of lexeme variants on maps of a dialect atlas, Altmann (1985) used the birth-and-death process based on the following assumptions: | ||
| − | (a) In a time interval | + | (a) In a time interval Δ<math>t</math> the birth of a new variant is proportional to the length of the interval, i.e. <math>a</math>Δ<math>t</math>. |
| − | (b) The assertion of a variant against x rivals is propotional to the number of rivals and the length of the interval, i.e. | + | (b) The assertion of a variant against <math>x</math> rivals is propotional to the number of rivals and the length of the interval, i.e. <math>bx</math>Δ<math>t</math>. |
| − | (c) The death of a variant is proportional to the number of variants and the length of the interval, i.e. | + | (c) The death of a variant is proportional to the number of variants and the length of the interval, i.e. <math>cx</math>Δ<math>t</math>. |
| − | (d) No change (birth, death or assertion) in | + | (d) No change (birth, death or assertion) in Δ<math>t</math> is given as the complement to the above changes: 1 – [<math>a+(b+c)x</math>]Δ<math>t</math>, ignoring intervals smaller then Δ<math>t</math>. |
(e) The events are independent and the probability of more then one event in the interval is zero. | (e) The events are independent and the probability of more then one event in the interval is zero. | ||
| − | Thus the probability that there are x-1 variants and a new variant arises or asserts itself against x-1 rivals is | + | Thus the probability that there are <math>x-1</math> variants and a new variant arises or asserts itself against <math>x-1</math> rivals is |
<math>a\triangle tP_{x-1}(t) + b(x-1)\triangle tP_{x-1}(t)</math>; | <math>a\triangle tP_{x-1}(t) + b(x-1)\triangle tP_{x-1}(t)</math>; | ||
| − | the probability that there are x+1 variants and one dies is | + | the probability that there are <math>x+1</math> variants and one dies is |
<math>c(x+1)\triangle tP_{x+1}(t)</math>; | <math>c(x+1)\triangle tP_{x+1}(t)</math>; | ||
| − | the probability that nothing happens in | + | the probability that nothing happens in Δ<math>t</math> is |
<math>{{1-[a+(b+c)x]\triangle t}}P_x(t)</math>. | <math>{{1-[a+(b+c)x]\triangle t}}P_x(t)</math>. | ||
| − | Putting these probabilities together we obtain the probability that in the interval (t, t+ | + | Putting these probabilities together we obtain the probability that in the interval (<math>t</math>, <math>t</math>+Δ<math>t</math>) there will be exactly <math>x</math> variants as |
<math>P_x(t+\triangle t) = [a+b(x-1)]\triangle tP_{x-1}(t) + c(x+1)\triangle tP_{x+1}(t) + {1-[a+(b+c)x]\triangle t}P_x(t)</math>. | <math>P_x(t+\triangle t) = [a+b(x-1)]\triangle tP_{x-1}(t) + c(x+1)\triangle tP_{x+1}(t) + {1-[a+(b+c)x]\triangle t}P_x(t)</math>. | ||
| − | Substracting | + | Substracting <math>P_x</math> from both sides and dividing them by Δ<math>t</math>, we obtain |
<math>\frac{P_x(t+\triangle t)-P_x(t)}{\triangle t}= [a+b(x-1)P_{x-1}(t)+c(x+1)P_{x+1}(t)-[a+(b+c)x]P_x(t)]</math>. | <math>\frac{P_x(t+\triangle t)-P_x(t)}{\triangle t}= [a+b(x-1)P_{x-1}(t)+c(x+1)P_{x+1}(t)-[a+(b+c)x]P_x(t)]</math>. | ||
| − | Letting <math>\triangle t\rightarrow 0</math> we finally | + | Letting <math>\triangle t\rightarrow 0</math> we finally get |
<math>\frac{dP_x(t)}{dt}=[a+b(x-1)P_{x-1}(t)+c(x+1)P_{x+1}(t)-[a+(b+c)x]P_x(t)]</math> | <math>\frac{dP_x(t)}{dt}=[a+b(x-1)P_{x-1}(t)+c(x+1)P_{x+1}(t)-[a+(b+c)x]P_x(t)]</math> | ||
| Line 148: | Line 148: | ||
and setting b/c = q and a/b = k results again in the negative binomial distribution | and setting b/c = q and a/b = k results again in the negative binomial distribution | ||
| − | (4)<math>P_x=\begin{pmatrix}k&+&x&-&1\\&&x\end{pmatrix}p^kq^x, \quad x=0,1,2,...</math> | + | (4) <math>P_x=\begin{pmatrix}k&+&x&-&1\\&&x\end{pmatrix}p^kq^x, \quad x=0,1,2,...</math> |
| − | For dialect maps, (4) is to be understood as the probability that the basic lexeme has x variants, i.e. if on a map there is only one unique form, then x = 0. | + | For dialect maps, (4) is to be understood as the probability that the basic lexeme has <math>x</math> variants, i.e. if on a map there is only one unique form, then <math>x</math> = 0. |
'''Example: Goebl´s law (dialectal diversification)''' | '''Example: Goebl´s law (dialectal diversification)''' | ||
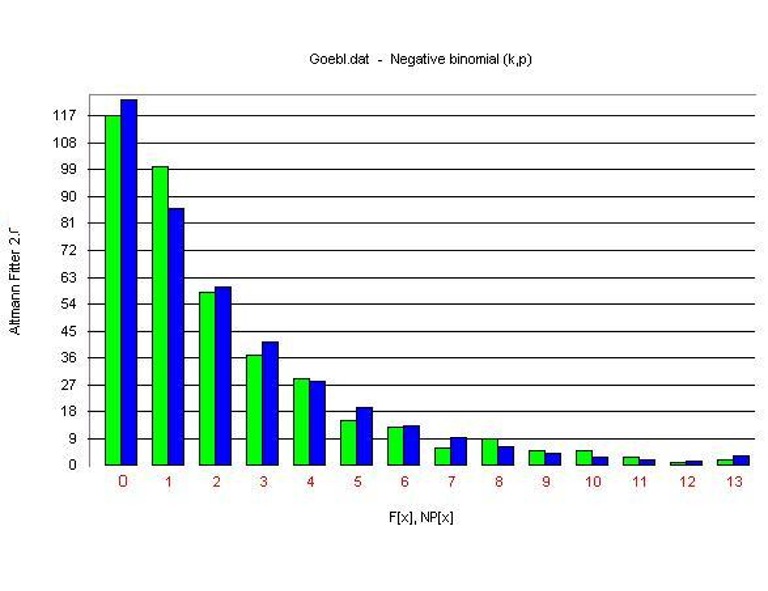
| − | Goebl (1984) studied the dialect maps of North West France and Italy and brought the distribution of the numbers of variants in the atlases. Since dialectal variants of a concept arise by a birth-and-death process, the number of maps containing x variants must follow the negative binomial distribution. One of these distributions is shown in Table 1 (Fig. 1). | + | Goebl (1984) studied the dialect maps of North West France and Italy and brought the distribution of the numbers of variants in the atlases. Since dialectal variants of a concept arise by a birth-and-death process, the number of maps containing <math>x</math> variants must follow the negative binomial distribution. One of these distributions is shown in Table 1 (Fig. 1). |
| Line 168: | Line 168: | ||
'''Example: Beöthy´s law (semantic diversification)''' | '''Example: Beöthy´s law (semantic diversification)''' | ||
| − | According to this law ''the ranked frequencies of the elements of a semantic class are distributed according'' to (3) or (5) (see below). Rothe (1991c) brings a survey of semantic classes abiding by these laws. Testing has been perfomed for meanings of different Hungarian verbal prefixes (Beöthy, Altmann 1984a,b, 1991), Slovak verbal prefixes (Nemcová 1991), the Japanese postposition ni (Roos 1991), German compounds (Raether, Rothe 1991), the German particle ''von'' (Best 1991), the German preposition ''auf'' (Fuchs 1991), the English preposition ''in'' (Hennern 1991), the Polish preposition ''w'' (Hammerl, Sambor 1991), Russian conjunctions ''a'' and ''no'' (Kuße 1991), the French conjunction ''et'' (Rothe 1986), the German genitive (Rothe 1991b), word class distribution in Latin, German and Chinese (Schweers, Zhu 1991), in German (Best 1994, 1997b, 2000b, 2001e; Hammerl 1989; Judt 1995), in Arabic (Altmann 1991a), in Portuguese (Ziegler 1998, 2001), in French (Judt 1995), spelling errors by Japanese English-users (Rothe | + | According to this law ''the ranked frequencies of the elements of a semantic class are distributed according'' to (3) or (5) (see below). Rothe (1991c) brings a survey of semantic classes abiding by these laws. Testing has been perfomed for meanings of different Hungarian verbal prefixes (Beöthy, Altmann 1984a,b, 1991), Slovak verbal prefixes (Nemcová 1991), the Japanese postposition ni (Roos 1991), German compounds (Raether, Rothe 1991), the German particle ''von'' (Best 1991), the German preposition ''auf'' (Fuchs 1991), the English preposition ''in'' (Hennern 1991), the Polish preposition ''w'' (Hammerl, Sambor 1991), Russian conjunctions ''a'' and ''no'' (Kuße 1991), the French conjunction ''et'' (Rothe 1986), the German genitive (Rothe 1991b), word class distribution in Latin, German and Chinese (Schweers, Zhu 1991), in German (Best 1994, 1997b, 2000b, 2001e; Hammerl 1989; Judt 1995), in Arabic (Altmann 1991a), in Portuguese (Ziegler 1998, 2001), in French (Judt 1995), spelling errors by Japanese English-users (Rothe 1991c), word building patterns in Early High German (Best 1990). |
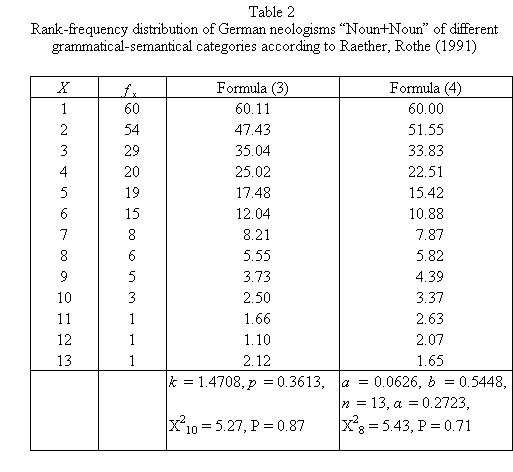
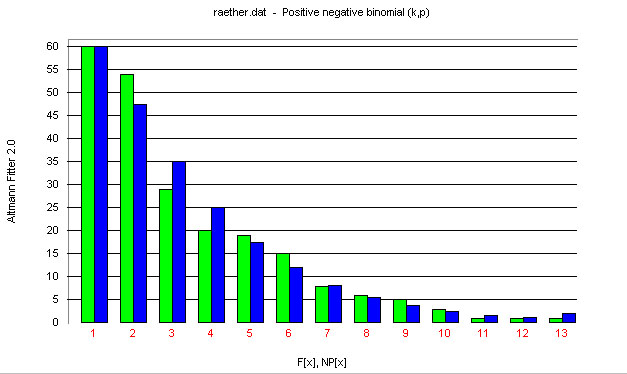
In the example (Table 2, Fig. 2) one finds the ranked distribution of German neologisms of the type “Noun + Noun” categorized in 13 groups from Raether, Rothe (1991). | In the example (Table 2, Fig. 2) one finds the ranked distribution of German neologisms of the type “Noun + Noun” categorized in 13 groups from Raether, Rothe (1991). | ||
| Line 184: | Line 184: | ||
Hřebíček used two assumptions: | Hřebíček used two assumptions: | ||
| + | |||
(i) The logarithm of the ratio of the probabilities <math>P_1</math> and <math>P_x</math> is proportional to the logarithm of the classe size, i.e | (i) The logarithm of the ratio of the probabilities <math>P_1</math> and <math>P_x</math> is proportional to the logarithm of the classe size, i.e | ||
| Line 194: | Line 195: | ||
yielding the solution | yielding the solution | ||
| − | (5)<math>P_x=P_1x^{-(a+b\ln x)}, \quad x=1,2,3,...</math>. | + | (5) <math>P_x=P_1x^{-(a+b\ln x)}, \quad x=1,2,3,...</math>. |
| − | If (5) is considered a probability distribution, then | + | If (5) is considered a probability distribution, then <math>P_1</math> is the norming constant, otherwise it is estimated as the size of the first class (<math>x</math> = 1). Since the frequency of the first class <math>x</math> = 1 is decisive for the form of the distribution, one usually ascribes it a special value α, modifying (5) as |
| − | (6)<math>P_x=\begin{cases} | + | (6) <math>P_x=\begin{cases}\alpha, & x=1\\\frac{(1-a)x^{(a+b\ln x)}}{T}, & x=2,3,...,(n)\end{cases}</math> |
| − | where <math>T=\sum_{j=2}^nj^{-(a+b\ln j)}</math>, 0 < α < 1, <math>a,b\in\mathfrak{R}</math> so that <math>P_x</math> converges for <math>n\rightarrow\infty</math>. This version corroborates again the relevance of Menzerath´s law (<math>\rightarrow</math>). Distributions (5) or (6) are called ''Zipf-Alekseev distributions''. If | + | where <math>T=\sum_{j=2}^nj^{-(a+b\ln j)}</math>, 0 < α < 1, <math>a,b\in\mathfrak{R}</math> so that <math>P_x</math> converges for <math>n\rightarrow\infty</math>. This version corroborates again the relevance of Menzerath´s law (<math>\rightarrow</math>). Distributions (5) or (6) are called ''Zipf-Alekseev distributions''. If <math>n</math> is finite, (6) is called ''modified right truncated Zipf-Alekseev distribution'' (see Wimmer, Altmann 1999). |
Even though (3) and (5) are quite different, it can be shown that they are special cases of the Siromoney-Dirichlet distribution | Even though (3) and (5) are quite different, it can be shown that they are special cases of the Siromoney-Dirichlet distribution | ||
| − | (7)<math>P_x=\frac{a_xe^{-\theta b_x}}{f(\theta)}, \quad x=1,2,3,...</math> <math>f(\theta)=\sum_{j=1}^\infty a_je^{-\theta b_j}<\infty</math> | + | (7) <math>P_x=\frac{a_xe^{-\theta b_x}}{f(\theta)}, \quad x=1,2,3,...</math> <math>f(\theta)=\sum_{j=1}^\infty a_je^{-\theta b_j}<\infty</math> |
| − | (i) If <math>a_x = k^{(x)}/x!, b_x = x, e^{-\theta} = q\quad</math>, we obtain the positive negative binomial distribution with parameters (k, p) (q = 1-p); | + | (i) If <math>a_x = k^{(x)}/x!, b_x = x, e^{-\theta} = q\quad</math>, we obtain the positive negative binomial distribution with parameters (<math>k</math>,<math>p</math>) (<math>q = 1-p</math>); |
| − | (ii) if <math>\theta = 1, a_x = 1, b_x = (a+b \quad\ln \quad x)\ln x</math>, we obtain the Zipf-Alekseev distribution (a,b); | + | (ii) if <math>\theta = 1, a_x = 1, b_x = (a+b \quad\ln \quad x)\ln x</math>, we obtain the Zipf-Alekseev distribution (<math>a,b</math>); |
(iii) the 1-displaced negative binomial distribution, which would be obtained with the conventional displacement of (4), would result if <math>a_x = k^{(x-1)}/(x-1)!, b_x = x-1, e^{-\theta} = q\quad</math>. | (iii) the 1-displaced negative binomial distribution, which would be obtained with the conventional displacement of (4), would result if <math>a_x = k^{(x-1)}/(x-1)!, b_x = x-1, e^{-\theta} = q\quad</math>. | ||
| Line 218: | Line 219: | ||
The connotations of a word diversify because everybody can have different associations. Nevertheless, within a community of speakers, they are distributed in a very regular way suggesting a background mechanism which can be captured as a law. | The connotations of a word diversify because everybody can have different associations. Nevertheless, within a community of speakers, they are distributed in a very regular way suggesting a background mechanism which can be captured as a law. | ||
| − | In the dictionaries of word associations (see e.g. Palermo, Jenkins 1964), the responses to a stimulus word are ordered according to the number of test persons that gave the same response, i.e. they are ranked according to their frequency of occurrence. The | + | In the dictionaries of word associations (see e.g. Palermo, Jenkins 1964), the responses to a stimulus word are ordered according to the number of test persons that gave the same response, i.e. they are ranked according to their frequency of occurrence. The persons tested are usually classified according to age, sex, education, occupation, social status etc. Quantitative modelling began most probably in Horvath (1963) and continued in Haight (1966), Haight, Jones (1974), Lánský, Radil-Weiss (1980) who used the logarithmic, the Yule, the Borel and the Haight-zeta distributions, none of which gave satisfactory results. Dolinskij (1988, 1994) proposed the Zipf-Alekseev distribution, Altmann (1992) added the 1-displaced negative binomial and modified the Zipf-Alekseev distributions. |
In Table 3 (Figure 3) one finds the fitting of the Zipf-Alekseev distribution to the rank-frequency of associations of the word “high” (4th grade, male) as given by Palermo, Jenkins (1964). | In Table 3 (Figure 3) one finds the fitting of the Zipf-Alekseev distribution to the rank-frequency of associations of the word “high” (4th grade, male) as given by Palermo, Jenkins (1964). | ||
Latest revision as of 13:23, 15 June 2009
1. Problem and history
Diversification is a process of enlarging the number of forms or meanings of any linguistic entity. It can be paradigmatic, e.g. the rise of cases, numbers, tenses, etc., phono-morphemic, e.g. the rise of allophones, allomorphs etc., geographical, e.g. the increase in the number of different expressions of a concept, social, e.g. the rise of different words or meanings of a word or different pronunciations, idiolectal within a community, semantic, e.g. the increase in synonymy and polysemy, contextual, e.g. the increase in the usage of a unit in different contexts. Diversification comprises a number of phenomena dispersed in this volume.
For the sake of illustration let us show some concrete examples:
1) The word can enlarge its class membership without any change, e.g. through conversion: “the hand”, “to hand”.
2) The stem enlarges its class membership through derivation, e.g. German "Bild", "bilden", "bildhaft", or vocalization in Semitic languages, etc.
3) The stem can enlarge its applicability within one class through derivation e.g. German "Blut", "Blutung", "Bluter", or through vocalization, etc.
4) The stem can enlarge its applicability within one class through compounding e.g. "Blut", "Blutdruck", "Blutdurst", etc.
5) If a language abandons isolating morphology, then morphemes diversify into several morphs because of agglutination or inflection (sequential or syntactic dependence).
6) The word can enlarge its applicability in the sentence by acquiring several functions, i.e. it enlarges its dispositional properties, which are different from the constant grammatical properties, e.g. practically every word can become the subject of a sentence.
7) Verbs can enlarge their valence, i.e. their combinability with different cases.
8) The word can enlarge its cotextuality (cf. Köhler 1986), i.e. its ability to occur in several contexts (where "context" can be defined in several ways). The reverse of this kind of diversification process is part of style formation, where a "position" diversifies, i.e., a position in a given context can be filled with different units (words, sentences, etc.).
9) A concept can be expressed by different forms, giving rise to dialects, sociolects, idiolects, or to synonymy.
10) A word can acquire different meaning (polysemy).
11) Every word can acquire different associations (connotations).
Diversified entities abide by a ranking law, i.e. if the members of the diversified entity are ordered according to their frequency, then the frequencies are “lawfully” connected.
The factors of diversification can be as follows (Altmann 2005):
a) Random fluctuation which is omnipresent in any language phenomena.
b) Environmentally conditioned variation forcing an element to acquire different forms or meaning nuances in different environments.
c) Conscious change through conscious creation, borrowing, emotionality etc.
d) Self-organisatory triggering of a process to a limit, causing changes on other levels, too.
e) System modification joined with local or global modifications in a subsystem,
f) Köhlerian requirements (Köhler 1986, 1987, 1989, 1990, 1991) forcing to take into account collateral pressures form different sides. They are as follows: (i) The trend for minimal coding and deciding effort, (ii) sufficient redundancy, (iii) the coding requirement in general, (iv) context economy vs. context specificity, and (v) invariance vs. flexibility of relation between expression and meaning.
The concepts of diversification and unification go back to G.K. Zipf (1935, 1949). Together they are called “Zipfian processes”. The scope of the phenomena is enormous. Semantic phenomena have been examined by Beöthy and Altmann (1984a,b, 1991), Altmann (1985a), Altmann, Best, Kind (1987); grammatical phenomena were analyzed in the omnibus volume edited by Rothe (1991), where also a study on spelling errors in English can be found, and dialectal diversification was studied by Altmann (1985b).
The laws hold usually for ranked nominal classes of limited size.
2. Hypothesis
Every linguistic entity diversifies, i.e. it generates variants and secondary forms and acquires membership in different classes. The ranked frequencies of individual entities abide by a rank-frequency distribution (or a rank-frequency series).
A “rank-frequency distribution” (series) is a function expressing the decrease of frequencies ranked according to their magnitude. There are, eo ipso, no bell-shaped rank-frequency distributions.
“Variants” are all free or conditional “non-standard” forms of the entity, e.g. allophones, allomorphs, dialectal or sociolectal expressions of a concept, etc.
“Secondary forms” are in some way derived from the primary form, e.g. secondary meanings (polysemy), cases, times, moods, aspects, etc.
“Classes” are built by a class-building criterion, e.g. derivates, compounds, declination classes, word classes (Wortarten), even semantic classes, etc.
Corollary: If the above hypothesis holds, then the frequencies of elements of a linguistic class are not distributed uniformly.
In a “uniform distribution” all frequencies are equal. The corollary is rather a well corroborated inductive generalization. Some theoretical rank-frequency distributions can result in the discrete uniform distribution for special values of parameters but they are not actual in linguistics.
3. Derivation
3.1. Altmann´s approach A (1991).
Because the entities are ranked and because of the corollary, it is true that for the probabilities of classes it holds that
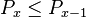
Since 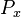 and
and 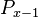 (
(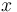 = 2,3,…) are joined in a law-like manner, we can write
= 2,3,…) are joined in a law-like manner, we can write
(1) 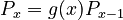 , where
, where 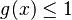 .
.
Furthermore, 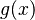 can be written as
can be written as
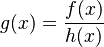 ,
,
where 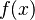 is a function composed of a language constant
is a function composed of a language constant 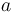 and the diversifying effect of the speaker
and the diversifying effect of the speaker 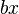 , i.e.
, i.e. 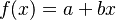 , while
, while 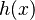 contains the controlling, regulating effect of the hearer (community)
contains the controlling, regulating effect of the hearer (community) 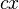 , i.e.
, i.e.
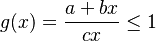 , (a, b, and c are assumed positive),
, (a, b, and c are assumed positive),
so that
(2) 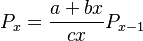 .
.
In order to obtain a known distribution, one can reparametrize (2) by writing 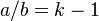 and
and 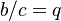 , and solving (2) for
, and solving (2) for 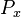 . One obtains
. One obtains
(3) 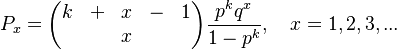
yielding the zero-truncated (positive) negative binomial distribution. The condition 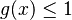 is fulfilled if
is fulfilled if 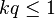 .
Using (1) Altmann (1991) showed a number of other possibilities of obtaining a diversification distribution.
.
Using (1) Altmann (1991) showed a number of other possibilities of obtaining a diversification distribution.
3.2. Alternative derivation (Altmann 1985b)
For the purposes of dialectal variation captured in terms of numbers of lexeme variants on maps of a dialect atlas, Altmann (1985) used the birth-and-death process based on the following assumptions:
(a) In a time interval Δ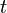 the birth of a new variant is proportional to the length of the interval, i.e.
the birth of a new variant is proportional to the length of the interval, i.e. 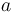 Δ
Δ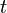 .
.
(b) The assertion of a variant against 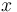 rivals is propotional to the number of rivals and the length of the interval, i.e.
rivals is propotional to the number of rivals and the length of the interval, i.e. 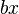 Δ
Δ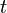 .
.
(c) The death of a variant is proportional to the number of variants and the length of the interval, i.e. 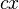 Δ
Δ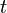 .
.
(d) No change (birth, death or assertion) in Δ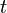 is given as the complement to the above changes: 1 – [
is given as the complement to the above changes: 1 – [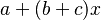 ]Δ
]Δ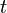 , ignoring intervals smaller then Δ
, ignoring intervals smaller then Δ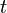 .
.
(e) The events are independent and the probability of more then one event in the interval is zero.
Thus the probability that there are 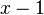 variants and a new variant arises or asserts itself against
variants and a new variant arises or asserts itself against 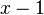 rivals is
rivals is
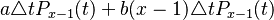 ;
;
the probability that there are 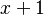 variants and one dies is
variants and one dies is
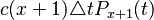 ;
;
the probability that nothing happens in Δ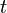 is
is
![{{1-[a+(b+c)x]\triangle t}}P_x(t)](/images/math/d/a/8/da843f8b1d3ceb3a66d30ebef301c100.png) .
.
Putting these probabilities together we obtain the probability that in the interval (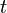 ,
, 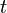 +Δ
+Δ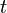 ) there will be exactly
) there will be exactly 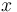 variants as
variants as
![P_x(t+\triangle t) = [a+b(x-1)]\triangle tP_{x-1}(t) + c(x+1)\triangle tP_{x+1}(t) + {1-[a+(b+c)x]\triangle t}P_x(t)](/images/math/0/c/e/0ce6b9bd7a96af104d0c71f083e0352d.png) .
.
Substracting 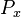 from both sides and dividing them by Δ
from both sides and dividing them by Δ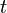 , we obtain
, we obtain
![\frac{P_x(t+\triangle t)-P_x(t)}{\triangle t}= [a+b(x-1)P_{x-1}(t)+c(x+1)P_{x+1}(t)-[a+(b+c)x]P_x(t)]](/images/math/5/6/2/56206777ddcbb1a3ba6d769a668a1866.png) .
.
Letting 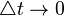 we finally get
we finally get
![\frac{dP_x(t)}{dt}=[a+b(x-1)P_{x-1}(t)+c(x+1)P_{x+1}(t)-[a+(b+c)x]P_x(t)]](/images/math/e/6/1/e619e986906dea55179cc09b28fbd157.png)
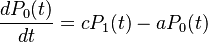
Solving the balancing equations holding for the steady state
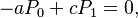
![-[a+(b+c)x]P_x+[a+b(x-1)]P_{x-1}+c(x+1)P_{x+1}=0, \quad x\ge 1,](/images/math/b/8/d/b8d43ad070ae4fc95dd5947dd928592a.png)
and setting b/c = q and a/b = k results again in the negative binomial distribution
(4) 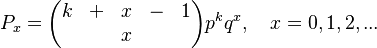
For dialect maps, (4) is to be understood as the probability that the basic lexeme has 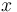 variants, i.e. if on a map there is only one unique form, then
variants, i.e. if on a map there is only one unique form, then 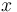 = 0.
= 0.
Example: Goebl´s law (dialectal diversification)
Goebl (1984) studied the dialect maps of North West France and Italy and brought the distribution of the numbers of variants in the atlases. Since dialectal variants of a concept arise by a birth-and-death process, the number of maps containing 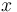 variants must follow the negative binomial distribution. One of these distributions is shown in Table 1 (Fig. 1).
variants must follow the negative binomial distribution. One of these distributions is shown in Table 1 (Fig. 1).
Example: Beöthy´s law (semantic diversification)
According to this law the ranked frequencies of the elements of a semantic class are distributed according to (3) or (5) (see below). Rothe (1991c) brings a survey of semantic classes abiding by these laws. Testing has been perfomed for meanings of different Hungarian verbal prefixes (Beöthy, Altmann 1984a,b, 1991), Slovak verbal prefixes (Nemcová 1991), the Japanese postposition ni (Roos 1991), German compounds (Raether, Rothe 1991), the German particle von (Best 1991), the German preposition auf (Fuchs 1991), the English preposition in (Hennern 1991), the Polish preposition w (Hammerl, Sambor 1991), Russian conjunctions a and no (Kuße 1991), the French conjunction et (Rothe 1986), the German genitive (Rothe 1991b), word class distribution in Latin, German and Chinese (Schweers, Zhu 1991), in German (Best 1994, 1997b, 2000b, 2001e; Hammerl 1989; Judt 1995), in Arabic (Altmann 1991a), in Portuguese (Ziegler 1998, 2001), in French (Judt 1995), spelling errors by Japanese English-users (Rothe 1991c), word building patterns in Early High German (Best 1990). In the example (Table 2, Fig. 2) one finds the ranked distribution of German neologisms of the type “Noun + Noun” categorized in 13 groups from Raether, Rothe (1991).
The result shows that nominal classifications of language entities abide by this type of diversification law.
3.3. Hřebíček ´s approach (1996)
Hřebíček used two assumptions:
(i) The logarithm of the ratio of the probabilities 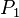 and
and 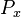 is proportional to the logarithm of the classe size, i.e
is proportional to the logarithm of the classe size, i.e
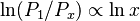
(ii) the proportionality function is given by the logarithm of Menzerath´s law ( Hierarchy), i.e.
Hierarchy), i.e.
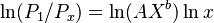 ,
,
yielding the solution
(5) 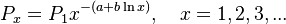 .
.
If (5) is considered a probability distribution, then 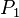 is the norming constant, otherwise it is estimated as the size of the first class (
is the norming constant, otherwise it is estimated as the size of the first class (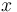 = 1). Since the frequency of the first class
= 1). Since the frequency of the first class 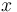 = 1 is decisive for the form of the distribution, one usually ascribes it a special value α, modifying (5) as
= 1 is decisive for the form of the distribution, one usually ascribes it a special value α, modifying (5) as
(6) 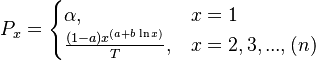
where 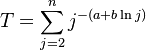 , 0 < α < 1,
, 0 < α < 1, 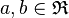 so that
so that 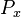 converges for
converges for 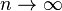 . This version corroborates again the relevance of Menzerath´s law (
. This version corroborates again the relevance of Menzerath´s law ( ). Distributions (5) or (6) are called Zipf-Alekseev distributions. If
). Distributions (5) or (6) are called Zipf-Alekseev distributions. If 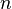 is finite, (6) is called modified right truncated Zipf-Alekseev distribution (see Wimmer, Altmann 1999).
Even though (3) and (5) are quite different, it can be shown that they are special cases of the Siromoney-Dirichlet distribution
is finite, (6) is called modified right truncated Zipf-Alekseev distribution (see Wimmer, Altmann 1999).
Even though (3) and (5) are quite different, it can be shown that they are special cases of the Siromoney-Dirichlet distribution
(7) 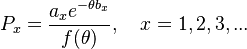
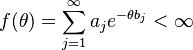
(i) If 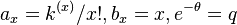 , we obtain the positive negative binomial distribution with parameters (
, we obtain the positive negative binomial distribution with parameters (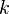 ,
,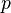 ) (
) (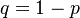 );
);
(ii) if 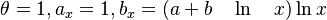 , we obtain the Zipf-Alekseev distribution (
, we obtain the Zipf-Alekseev distribution (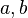 );
);
(iii) the 1-displaced negative binomial distribution, which would be obtained with the conventional displacement of (4), would result if 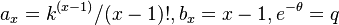 .
.
Formula (7) admits to the development of further theoretical approaches (see Wimmer, Altmann 1999).
Example: Association law
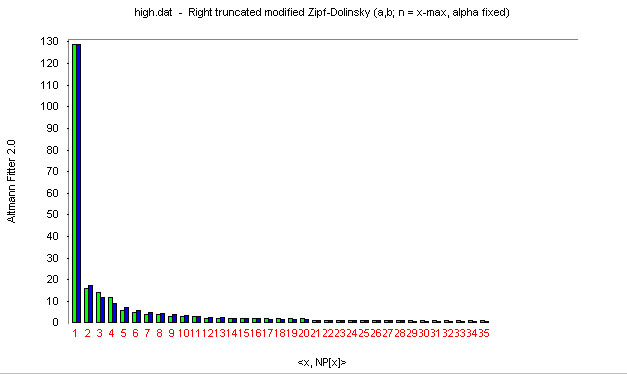
The connotations of a word diversify because everybody can have different associations. Nevertheless, within a community of speakers, they are distributed in a very regular way suggesting a background mechanism which can be captured as a law. In the dictionaries of word associations (see e.g. Palermo, Jenkins 1964), the responses to a stimulus word are ordered according to the number of test persons that gave the same response, i.e. they are ranked according to their frequency of occurrence. The persons tested are usually classified according to age, sex, education, occupation, social status etc. Quantitative modelling began most probably in Horvath (1963) and continued in Haight (1966), Haight, Jones (1974), Lánský, Radil-Weiss (1980) who used the logarithmic, the Yule, the Borel and the Haight-zeta distributions, none of which gave satisfactory results. Dolinskij (1988, 1994) proposed the Zipf-Alekseev distribution, Altmann (1992) added the 1-displaced negative binomial and modified the Zipf-Alekseev distributions. In Table 3 (Figure 3) one finds the fitting of the Zipf-Alekseev distribution to the rank-frequency of associations of the word “high” (4th grade, male) as given by Palermo, Jenkins (1964).
The result represents a perfect fit that has been found in all cases of associations.
Fig. 3. Fitting the Zipf-Alekseev distribution (5) to the word associations of “high”
4. Author: U. Strauss, G. Altmann
5. References
Alekseev, P. M. (1978), O nelinejnych formulirovkach zakona Cipfa. In: Piotrovskij, R.G. (ed.), Statistika reči i avtomatičeskij analiz teksta: 53-65. Moskva/Leningrad: Naučnyj sovet po kompleksnoj probleme “Kibernetika” AN SSSR.
Altmann, G. (1985a). Semantische Diversifikation. Folia Linguistica 19, 177-200.
Altmann, G. (1985b). Die Entstehung diatopischer Varianten. Ein stochastisches Modell. Zs. für Sprachwissenschaft 4, 139-155.
Altmann, G. (1991). Modelling diversification phenomena in language. In: Rothe 1991: 33-46.
Altmann, G. (1991a). Word class diversification of Arabic verbal roots. In: Rothe 1991: 57-59.
Altmann, G. (1992). Two models for word association data. Glottometrika 13, 105-120.
Altmann, G. (1996). Diversification processes of the word. Glottometrika 15, 102-111.
Altmann, G. (2005). Diversification processes. In: Köhler, R., Altmann, G., Piotrowski, R.G. (eds.), Handbook of Quantitative Linguistics: 646-658. Berlin: de Gryuter.
Altmann, G., Best, K.H., Kind, B. (1987). Eine Verallgemeinerung des Gesetzes der semantischen Diversifikation. Glottometrika 8, 130-139.
Becker, H. (1995). Die Wirtschaft in der deutschsprachigen Presse. Frankfurt: Lang.
Beöthy, E., Altmann, G. (1984a). The diversification of meaning of Hungarian verbal prefixes. II. ki-. Finnisch-Ugrische Mitteilungen 8, 29-37.
Beöthy, E., Altmann, G. (1984b). Semantic diversification of Hungarian verbal prefixes. III.föl-, el-, be-. Glottometrika 7, 73-100.
Beöthy, E., Altmann, G. (1991). The diversification of meaning of Hungarian verbal prefixes. I.meg-. In: Rothe, U. (ed) 1991: 60-66.
Best, K.-H. (1990). Die semantische Diversifikation eines Wortbildungsmusters im Frühneuhochdeutschen. Glottometrika 11, 107-110.
Best, K.-H. (1991). Von: Zur Diversifikation einer Partikel des Deutschen. In: Rothe U. (ed) 1991: 94-104.
Best, K.H. (1993). Zur Wortartenhäufigkeit in Texten deutscher Kurzprosa der Gegenwart. Glottometrika 15, 1993, 1-11.
Best, K.-H. (1994). Word class frequencies in contemporary German short prose texts. J. of Quantitative Linguistics 1, 144-147.
Best, K.-H. (1997). Zur Wortartenhäufigkeit in Texten deutscher Kurzprosa. Glottometrika 16, 276-285.
Best, K.-H. (2000). Verteilung der Wortarten in Anzeigen. Göttinger Beiträge zur Sprachwissenschaft 4, 37-51
Best, K.-H. (2001). Zur Gesetzmäßigkeit der Wortartenverteilungen in deutschen Pressetexten. Glottometrics 1, 1-26.
Best, K.-H. (2003). Quantitative Linguistik: eine Annäherung. 2nd ed. Göttingen: Peust & Gutschmidt.
Best, K.-H. (2007). Diversifikation bei Eigennamen. In: Grzybek, P., Köhler, R. (eds.), Exact Methods in the Study of language and Text: 21-31. Berlin: de Gruyter
Best, K.-H. (2008). Zur Diversifikation lateinischer und griechischer Hexameter. Glottometrics 17: 43-50.
Best, K.-H. (2009). Diversifikation des Phonems /r/ im Deutschen. Glottometrics 18: 26-31.
Brüers, N., Heeren, A. (2004). Plural-Allomorphe in Briefen Heinrich von Kleists. Glottometrics 7: 85-90.
Dolinskij, V.A. (1988). Raspredelenie reakcij v ekseprimentach po verbal´nym associacijam. Acta et Commentationes Universitatis Tartuensis 827, 80-101.
Dolinskij, V.A. (1994). Moscow Student´s word associations. In: 2nd International Confer ence on Quantitative Linguistics, September 20-24, 1994, Moscow: 66-68. Moscow: Lomonosov Moscow State University.
Fuchs, R. (1991). Semantische Diversifikation der deutschen Präposition auf. In: Rothe, U. (ed.) 1991: 105-115.
Goebl, H. (1984). Dialektometrische Studien I. Tübingen: Niememyer.
Haight, F.A. (1966). Some statistical problems in connection with word association data. J. of Mathematical Psychology 3, 217-233.
Haight, F.A., Jones, R.B. (1974). A probabilistic treatment of qualitative data with special reference to word association tests. J. of Mathematical Psychology 11, 237-244.
Hammerl, R. (1989). Untersuchungen zur Verteilung der Wortarten im Text. Glottometrika 11, 142-156.
Hammerl, R. (1991). Untersuchungen zur Struktur der Lexik: Aufbau eines lexikalischen Basismodells. Trier, WVT.
Hammerl, R., Sambor, J. (1991). Untersuchungen zur Verteilung der Bedeutungen der polyfunktionalen polnischen Präposition ‘w’ im Text. In: Rothe, U. (ed.), 1991: 127-137.
Hammerl, R., Sambor, J. (1993a). O statystycznych prawach jezykowych. Warszawa: Polskie Towarzystwo Semiotyczne.
Hennern, A. (1991). Zur semantischen Diversifikation von „in“ im Englischen. In: Rothe, U. (Hrsg.), Diversification processes in language: grammar: 116-126. Hagen: Rottmann.
Horvath, W.J. (1963). A stochastic model for word association tests. Psychological Review 70, 361-364.
Hřebíček, L. (1996). Word associations and text. Glottometrika 15, 12-17.
Jakubajtis, T.A. (1981). Časti reči i tipi tekstov. Riga: Zinatne.
Judt, B. (1995). Wortartenhäufigkeiten im Deutschen und Französischen. Göttinen: Staats examensarbeit.
Junger, J. (1989). Diversification in the modern Hebrew verbal system. Glottometrika 10, 71 99.
Kločkova, E.A. (1968). O raspredelenii klassov slov v nekotorych funkcional´nach stiljach russ kogo jazyka. In: Voprosy slavjanskogo jazykoznanija: 109-118. Saratov.
Köhler, R. (1986), Zur linguistischen Synergetik. Struktur und Dynamik der Lexik. Bochum: Bockmeyer.
Köhler, R. (1987), Systems theoretical linguistics. Theoretical Linguistics 14, 241-57.
Köhler, R. (1989). Linguistische Analyseebenen, Hierarchisierung und Erklärung im Modell der sprachlichen Selbstregulation. Glottometrika 11, 1-18 (Ed. L. Hřebíček). Bochum: Brockmeyer.
Köhler, R. (1990). Elemente der synergetischen Linguistik. In: Glottometrika 12, 179-187. (Ed. R.Hammerl). Bochum: Brockmeyer,.
Köhler, R. (1991). Diversification of coding methods in grammar. In: Rothe, U. (ed.), Diversification processes in language: Grammar: 47-55. Hagen: Rottman.
Köhler, R. (1991). Diversification of coding methods in grammar. In: Rothe, U. (Hrsg.), Diversification processes in language: grammar: 47-55. Hagen: Rottmann.
Krylov, Ju.K. (1982a).Ob odnoj paradigme lingvostatističeskich raspredelenij. Acta et Commentationens Universitatis Tartuensis 628, 80-102.
Krylov, Ju.K. (1982b). Eine Untersuchung statistischer Gesetzmäßigkeiten auf der paradigmatischen Ebene der Lexik natürlicher Sprachen. In: Guiter, H., Arapov, M.V. (eds.), Studies on Zipf´s law: 234-262. Bochum: Brockmeyer.
Kuße, H. (1991). A und no in N.M. Karamzins Pis´ma Russkogo Putesetvennika. In: Rothe, U. (ed.), Diversification processes in language: grammar: 173-182. Hagen: Rottmann.
Laufer, J., Nemcová, E. (2009). Diversifikation deutscher morphologischer Klassen. Glottometrics 18, 13-25.
Lánský, P., Radil-Weiss, T. (1980). A generalization of the Yule-Simon model, with special reference to word association tests and neural cell assembly formation. J. of Mathematical Psychology 21, 53-65.
Leopold, E. (1998). Stochastische Modellierung lexikalischer Evolutionsprozesse. Hamburg: Kovač.
Meuser, K., Schütte, J.M., Stremme, S. (2008). Pluralallomorphe in den Kurzgeschichten von Wolfdietrich Schnurre. Glottometrics 17, 12-17.
Nemcová, E. (1991). Semantic diversification of Slovak verbal prefixes. In: Rothe, U. (ed.), Diversification processes in language: grammar: 67-74. Hagen: Rottmann.
Palermo, D.S., Jenkins, J.J. (1964). Word association norms. Grade School through College. Minneapolis: University of Minnesota Press.
Pawlowski, A. (1999). The quantitative approach in cultural anthropology: Application of linguistic corpora in the analysis of basic colour terms. J. of Quantitative Linguistics 6, 222 234.
Popescu, I.-I., Altmann, G. (2008). On the regularity of diversification in language. Glottometrics 17, 94-108.
Popescu, I.-I., Kelih, E., Best, K.-H., Altmann, G. (2009). Diversification of the case. Glottometrics 18, 32-39.
Raether, A., Rothe, U. (1991). Diversifikation der deutschen Komposita. In: Rothe, U. (ed.) 1991: 85-91.
Roos, U. (1991). Diversifikation der japanischen Postposition “-ni”. In: Rothe, U. (ed.), Diversification processes in language: grammar: 75-82. Hagen: Rottmann.
Rothe, U. (1986). Die Semantik des kontextuellen et. Frankfurt: Lang.
Rothe, U. (1990). Verteilung der Suffixe denominaler Verben nach ihren semantischen Wortbildungsmustern. Glottometrika 12, 107-114.
Rothe, U. (1990a). Semantische Motivation der Genuszuweisung. Glottometrika 11, 95-106.
Rothe, U. (1990b). Semantische Beziehungen zwischen Präfixen deutscher denominaler Verben und der motivierenden Nomina. Glottometrika 11, 111-121.
Rothe, U. (ed.) (1991). Diversification processes in language: grammar. Hagen: Rottmann.
Rothe, U. (1991a). Diversification processes in grammar. An introduction. In: Rothe, U. (ed.), Diversification processes in language: grammar: 3-32. Hagen: Rottmann.
Rothe, U. (1991b). Diversification of the case in German: genitive. In: Rothe, U. (ed.), Diversification processes in language: grammar: 140-156. Hagen: Rottmann.
Rothe, U. (1991c). Distribution of spelling errors by Japanese English-users. In: Rothe, U. (ed.), Diversification processes in language: grammar: 168-171. Hagen: Rottmann.
Saukkonen, P., Haipus, M., Niemikorpi, A., Sulkala, H. (1979). Suomen kielen taajuussa nasto. A frequency dictionary of Finnish. Porvoo-Helsinki: Juva.
Schweers, A., Zhu, J. (1991). Wortartenklassifikation im Lateinischen, Deutschen und Chinesischen. In: Rothe U. 1991: 157-167.
Schweiger, F. (1987). Zu den Modellen der semantischen Diversifikation von G. Altmann. Folia Linguistica 21, 191-194.
Tiščenko, V. (1970). Častota častii movi v riznich funkcional´nych stiljach sučasnoj ukrains´koj movi. In: Pitanija strukturnoi leksikologii. Kiiv.
Tuldava, J. (1998). Probleme und Methoden der quantitativ-systemischen Lexikologie. Trier: WVT.
Wimmer, G., Altmann, G. (1999). Thesaurus of univariate discrete probability distributions. Essen: Stamm.
Ziegler, A. (1998b). Word class frequencies in Brazilian-Portuguese texts. J. of Quantitative Linguistics 5, 269-280.
Ziegler, A. (2001). Word class frequencies in Portuguese press texts. In: Uhlířová, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a linguistic paradigm: levels, constituents, con-structs. Festschrift in honour of Ludek Hřebíček: 295-312. Trier: WVT
Ziegler, A., Best, K.-H., Altmann, G. (2001). A contribution to text spectra. Glottometrics 1, 97-108.
Zipf, G. K. (1935). The psycho-biology of language. An introduction to dynamic philology. Boston: Houghton Mifflin.
Zipf, G.K. (1949). Human behavior and the principle of least effort. Cambridge: Addison Wesley.
Zsilka, T. (1974). Stilisztika és statisztika. Budapest.