Difference between revisions of "Char Complexity"
m |
|||
| Line 1: | Line 1: | ||
'''1. Problem and history''' | '''1. Problem and history''' | ||
| − | The complexity of Chinese characters can be measured in terms of the number of strokes. The stroke is a segment written with one uninterrupted movement. The question arises whether complexity follows a regular distribution. Evidently, this is a special case of (→) length distributions. The pertinent statements can be qualified as laws only if they hold for any types of ideograms but up to now no other writing systems have been examined. | + | The complexity of Chinese characters can be measured in terms of the number of strokes. The stroke is a segment written with one uninterrupted movement. The question arises whether complexity follows a regular distribution. Evidently, this is a special case of (→) length distributions. The pertinent statements can be qualified as laws only if they hold for any types of ideograms but up to now no other writing systems have been examined. |
| − | Sanada (1999) shows empirical data on the distribution of strokes in Japanese but does not present a model. Proceeding rather inductively Yu (2001) found that the distribution of character lengths in texts follows the 1-displaced binomial distribution. Previous studies (Herdan 1966, Bohn 1998) did not achieve this result. | + | |
| − | The distribution in texts and in the dictionary may be quite different because in texts repetition is taken into account. The measurement in terms of the number of strokes is | + | Sanada (1999) shows empirical data on the distribution of strokes in Japanese but does not present a model. Proceeding rather inductively, Yu (2001) found that the distribution of character lengths in texts follows the 1-displaced binomial distribution. Previous studies (Herdan 1966, Bohn 1998) did not achieve this result. |
| − | Another kind of complexity of script, in which not only the number of the composing entities but also the | + | |
| + | The distribution in texts and in the dictionary may be quite different because in texts repetition is taken into account. The measurement in terms of the number of strokes is – as a matter of fact – the measurement of length, not that of complexity. | ||
| + | |||
| + | Another kind of complexity of script, in which not only the number of the composing entities is relevant, but also the way they ared joined together, can be measured according to Altmann (2004) but until now no testing has been performed. | ||
'''2. Hypothesis''' | '''2. Hypothesis''' | ||
| Line 16: | Line 19: | ||
Solving a (reparametrized) recurrence relation which is a special case of length distributions, namely | Solving a (reparametrized) recurrence relation which is a special case of length distributions, namely | ||
| − | (1)<math>P_{x+1} = \frac{n-x+1}{x}\frac{p}{q}, \quad x = 1, 2, ..., n+1</math> | + | (1) <math>P_{x+1} = \frac{n-x+1}{x}\frac{p}{q}, \quad x = 1, 2, ..., n+1</math> |
one obtains | one obtains | ||
| − | (2)<math>P_x = {n \choose x-1}p^{x-1}q^{n-x+1}, \quad x= 1,2,...,n+1, \quad 0<p<1, n\epsilon N</math> | + | (2) <math>P_x = {n \choose x-1}p^{x-1}q^{n-x+1}, \quad x= 1,2,...,n+1, \quad 0<p<1, n\epsilon N</math> |
'''Example''': Chinese characters in texts | '''Example''': Chinese characters in texts | ||
Revision as of 12:06, 16 June 2009
1. Problem and history
The complexity of Chinese characters can be measured in terms of the number of strokes. The stroke is a segment written with one uninterrupted movement. The question arises whether complexity follows a regular distribution. Evidently, this is a special case of (→) length distributions. The pertinent statements can be qualified as laws only if they hold for any types of ideograms but up to now no other writing systems have been examined.
Sanada (1999) shows empirical data on the distribution of strokes in Japanese but does not present a model. Proceeding rather inductively, Yu (2001) found that the distribution of character lengths in texts follows the 1-displaced binomial distribution. Previous studies (Herdan 1966, Bohn 1998) did not achieve this result.
The distribution in texts and in the dictionary may be quite different because in texts repetition is taken into account. The measurement in terms of the number of strokes is – as a matter of fact – the measurement of length, not that of complexity.
Another kind of complexity of script, in which not only the number of the composing entities is relevant, but also the way they ared joined together, can be measured according to Altmann (2004) but until now no testing has been performed.
2. Hypothesis
The distribution of the complexity of Chinese characters follows a usual length distribution.
Complexity = here the number of strokes in a Chinese sign.
3. Derivation
Solving a (reparametrized) recurrence relation which is a special case of length distributions, namely
(1) 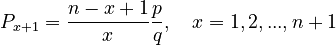
one obtains
(2) 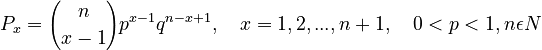
Example: Chinese characters in texts
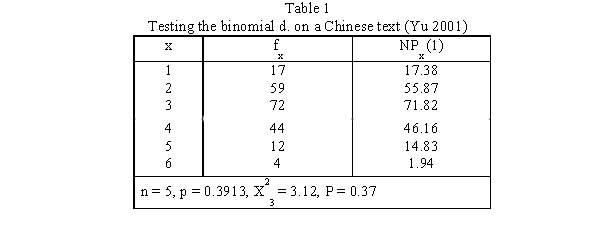
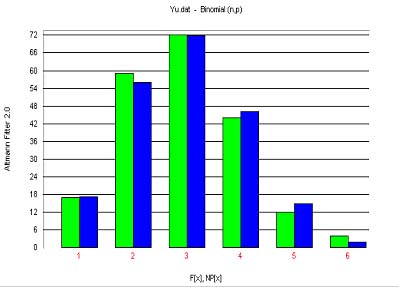
Yu (2001) tested the above hypothesis on 20 Chinese texts, one of which can be found in Table 1 and Fig. 1.
The result corroborates the hypothesis.
4. Authors: U. Strauss, G. Altmann
5. References
Altmann, G. (2004). Script complexity. Glottometrics 8, 68-74.
Bohn, H. (1998). Quantitative Untersuchungen der modernen chinesischen Sprache und Schrift. Hamburg: Kováč.
Bohn, H.(2002). Untersuchungen zur chinesischen Sprache und Schrift. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 127-177. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/
Herdan, G. (1966). The advanced theory of language as choice and chance. Berlin: Springer.
Menzel, C. (2002). Das synergetische Basismodell der Lexik und die chinesische Schrift. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 179-207. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/
Sanada, H. (1999). Analysis of Japanese vocabulary by the theory of synergetic linguistics. J. of Quantitative Linguistics 6, 239-251.
Yu, X. (2001). Zur Komplexität chinesischer Schriftzeichen. Göttinger Beiträge zur Sprachwissenschaft.5, 121-129.