Difference between revisions of "Rhythmic units"
| Line 40: | Line 40: | ||
| − | '''3.2. The birth process with repulsion''' | + | '''3.2. The birth process with repulsion''' (Lehfeldt 2003) |
Let the gaps between accentuated syllables are considered as urns and the non-accentuated as balls. In time interval h (time is merely an auxiliary variable) either 1 or none ball is inserted in an urn or before the first and behind the last one. Let the assumptions of the Poisson process pure birth process are fulfilled. The urns are not passive but exert influence on the acception of balls, namely the more balls are in the urn, the more the urn repulses new balls: a balanced rhythm requires a restricted number of non-accentuated syllables. Let the birth rate be <math>\lambda_x = n-x</math>. Then one obtains | Let the gaps between accentuated syllables are considered as urns and the non-accentuated as balls. In time interval h (time is merely an auxiliary variable) either 1 or none ball is inserted in an urn or before the first and behind the last one. Let the assumptions of the Poisson process pure birth process are fulfilled. The urns are not passive but exert influence on the acception of balls, namely the more balls are in the urn, the more the urn repulses new balls: a balanced rhythm requires a restricted number of non-accentuated syllables. Let the birth rate be <math>\lambda_x = n-x</math>. Then one obtains | ||
| Line 102: | Line 102: | ||
'''Kaßel, A.''' (2002). ''Zur Verteilung rhythmischer Einheiten in deutschen und englischen Texten''. Staatsexamensarbeit; Göttingen. | '''Kaßel, A.''' (2002). ''Zur Verteilung rhythmischer Einheiten in deutschen und englischen Texten''. Staatsexamensarbeit; Göttingen. | ||
| + | |||
| + | '''Lehfeldt, W.''' (2003). ''Akzent und Betonung im Russischen''. München: Sagner. | ||
'''Marbe, K.''' (1904). ''Über den Rhythmus der Prosa''. Giessen: J.Ricker´sche Verlagsbuchhandlung. | '''Marbe, K.''' (1904). ''Über den Rhythmus der Prosa''. Giessen: J.Ricker´sche Verlagsbuchhandlung. | ||
Revision as of 12:00, 4 July 2006
1. Problem and history
A rhythmic unit is according to Marbe (1904) the number of non-stressed syllables between two stressed ones. Some researchers consider it as a whole consisting of a stressed and the following non-stressed syllables. The problem is to ascertain whether the length of rhythmic units abides by a special distribution. The first numerical examinations have been performed by Marbe and Roetteken (1904). Best (2001c) assigns this problem to the “length” problems using the appropriate way of modelling. Brainerd – in another context – considered it a Markov chain. Lehfeldt and Altmann (2003) derive the model from an urn approach considering the Poissonian gap filling between accentuated syllables as a pure birth process with repulsion. Rhythmic units were used in the study of language acquisition by children (Deußig 1927/1969).
2. Hypothesis
The distribution of rhythmic units follows a regular probability distribution.
3. Derivation
3.1. Best´s approach
Best starts from the usual “length approach” considering the proportionality between frequency classes, i.e.
(1)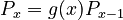 .
.
Setting g(x) = a/(b+x) and the necessary displacement which is conventional he obtains
(2)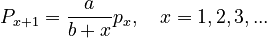
whose solution yields the 1-displaced hyper-Poisson distribution
(3)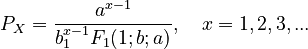
where 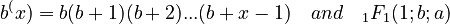
is the confluent hypergeometric function. The hyper-Poisson is a special case of the unified theory ( ) when
) when 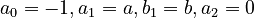 .
.
Example: Rhythmic units in German
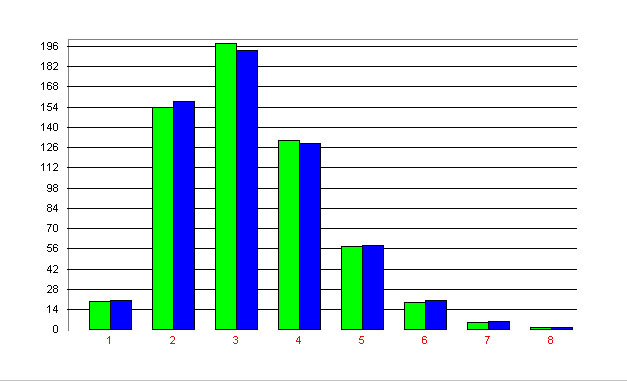
Best (2001c) examined 8 texts processed by Marbe and Roetteke and obtained in 6 cases a corroboration of the model. One of the results can be seen in Table 1 and Fig.1
3.2. The birth process with repulsion (Lehfeldt 2003)
Let the gaps between accentuated syllables are considered as urns and the non-accentuated as balls. In time interval h (time is merely an auxiliary variable) either 1 or none ball is inserted in an urn or before the first and behind the last one. Let the assumptions of the Poisson process pure birth process are fulfilled. The urns are not passive but exert influence on the acception of balls, namely the more balls are in the urn, the more the urn repulses new balls: a balanced rhythm requires a restricted number of non-accentuated syllables. Let the birth rate be 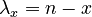 . Then one obtains
. Then one obtains
(4)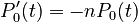
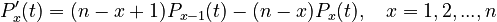 .
.
Solving (4) with boundary conditions 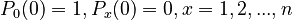 and substituting at last
and substituting at last 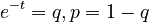 we obtain the binomial distribution
we obtain the binomial distribution
(5)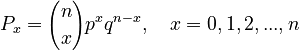
Brainerd (1976) considered sequences of this kind as Markov chains and obtained for the distances chains of different order represented by the modified geometric distribution (see Gap formation). Since in all models of order higher than zero the first class is modified, Lehfeldt and Altmann (2003) modified it a posteriori, too, and obtained the extended positive binomial distribution
(6)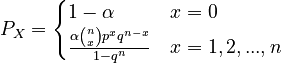
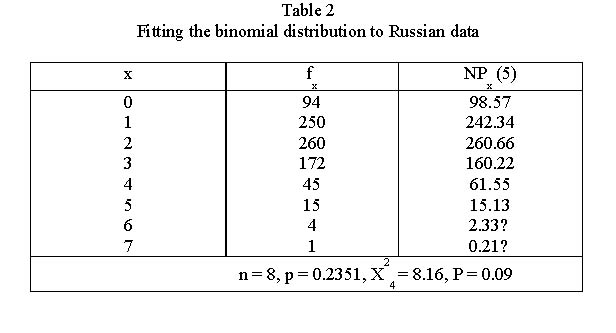
Evidently, (5) and (6) are identical when α = 1-qn. Example: Intervalls of non-accentuated syllables in Russian
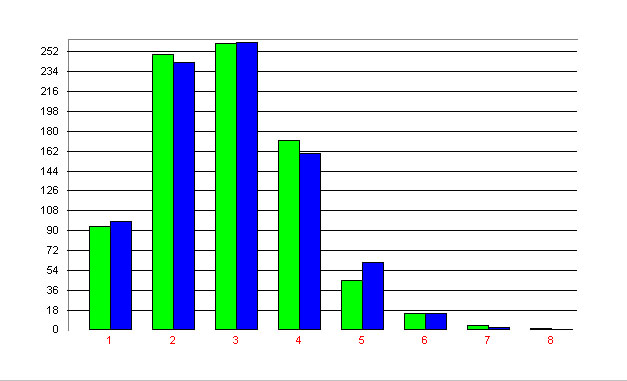
Lehfeldt and Altmann (2003) examined the intervals of non-accentuated syllables in Russian and obtained the results in Table 2 and Fig. 2. Here the rhythmic unit is merely the number of non-accentuated syllables.
The result of fitting is satisfactory. Additional pooling had brought still better results.
Example: Rhythmic units in Puschkins Werk “Vystrel”
Lehfeldt and Altmann (2003) fitted the extended positive binomial distribution to the rhythmic units in Puschkins work “Vystrel” and obtained the results presented in Table 3 and Fig. 3.
[[[Auch EPPO, Hype, Hpas, EpBin, Bin]] Wird eingetragen! Please complete
4. Authors: U. Strauss, G. Altmann, K.-H. Best
5. References
Best, K.-H. (2001a). Zur Verteilung rhythmischer Einheiten in deutscher Prosa. In: Best, K.H. (ed.), Häufigkeitsverteilungen in Texten: 162-166. Göttingen: Peust & Gutschmidt.
Best, K.-H. (2001b). Probability distributions of language entities. J. of Quantitative Linguistics 8, 1-11.
Best, K-H. (2002). The distribution of rhythmic units in German short prose. Glottometrics 3, 136-142.
Best, K.-H. (2005). Längen rhythmischer Einheiten. In: Altmann, G., Köhler, R., Piotrowski, R. (Hg.), Quantitative Linguistik - Quantitative Linguistics. Ein internationales Handbuch: 208-214. Berlin/ N.Y.: de Gruyter.
Best, K.-H. (2005). Karl Marbe (1869-1953). Glottometrics 9, 74-76".
Best, K.-H., Kotrasch, B. (2005). Albert Thumb (1965-1915). Glottometrics 9, 82-84.
Brainerd, B. (1976). On the Markov nature of text. Linguistics 176, 5-30.
Deußing, H. (1927/1969). Der sprachliche Ausdruck des Schulkindes. In: Helmers, H. (ed.), Zur Sprache des Kindes: 60-131. Darmstadt: Wissenschaftliche Buchgesellschaft.
Gropp, F. (1915). Zur Ästhetik und Statistik des Prosarhythmus. Würzburg, diss.phil.
Kaßel, A. (2002). Zur Verteilung rhythmischer Einheiten in deutschen und englischen Texten. Staatsexamensarbeit; Göttingen.
Lehfeldt, W. (2003). Akzent und Betonung im Russischen. München: Sagner.
Marbe, K. (1904). Über den Rhythmus der Prosa. Giessen: J.Ricker´sche Verlagsbuchhandlung.
Thumb, A. (1913). Satzrhythmus und Satzmelodie in der altgrichischen Prosa. In: Marbe, K. unter Mitwirkung von W. Peters, Fortschritte der Psychologie und ihrer Anwendungen I, 3, 139-168. Leipzig/Berlin: Teubner.