Vowel duration

1. Problem and history

In speech, vowel duration is not constant but varies at every occasion of pronouncing the given vowel. Phoneticians found a number of conditions under which a vowel is pronounced longer or shorter, e.g. position in the word, accent, length of the word (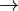$\rightarrow$ Hierarchy), phonological length etc. Geršiċ and Altmann (1988) tried to show that the distribution of durations for an individual speaker is lawlike, i.e. that there is a mechanism controlling the durations. Their derivation is shown below.

2. Hypothesis

The length of vowels in speech is regularly distributed in dependence on different local, global and momentaneuos factors.

3. Derivation

The duration of vowels is influenced by three different kinds of forces:

(a) Forces responsible for innovation, emotionality, need for expression etc. leading to fluctuation, i.e. deviation from norms and self-organization. This is the class of Bühler´s expression function (Bühler 1934), Zipf´s diversification (Zipf 1949) etc.

(b) Forces fixing or modifying locally or globally the vowel duration, like phonological norms (short, long), suprasegmentals (tone, accent) and combinatorial factors (neighbour-hood).

(c) Forces restricting the speaker, damping the fluctuation, caring for equilibria like Bühler´s representation function, Zipf´s unification, pressure or control of the community.

Let

x = duration f(x) = the probability fucntion of duration S = expressive force of the speaker B = accentuation F = phonological length K = quantity of the following consonant H = the controlling force of the community

then

(1)$\frac{f'(x)}{f(x)}= \frac{Sx + Bx + F + K/x}{Hx}$.

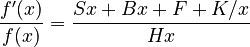Setting (S+B)/H = a, F/(S+B) = b, K/(S+B) = c one obtains

(2)$\frac{d[f(x)]}{f(x)}= \left( a + \frac{ab}{x} + \frac{ac}{x^2} \right)dx$

resulting in

(3)$f(x) = Nx^{ab}e^{ax-ac/x}, \quad 0 < x < R$

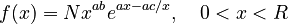
which can be simply written as (A = ab, B = a, C = -ac)

(4)$f(x) = Nx^A e^{Bx+C/x}, \quad 0 < x < R$

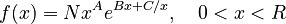
where N is the normalizing constant. It can easily be seen that this is just a special case of formula (2) and (3) of the unified theory ($\rightarrow$).

Example. Vowel duration in Batschka-German

Geršiċ and Altmann (1988) measured the duration of five categories of vowels (short non-ac-centuated, short semi-accentuated, short accentuated, long semi-accentuated, long accentuat-ed) with three speakers of Batschka-German. The duration was measured in intervals of 20 milliseconds, i.e. 20-39, 40-59, 60-79,… and transformed in X = X´/20 so that they obtained intervals 1,2), 2,3),… The probability in the interval was computed by numerical integration and optimization. Table 1 and Fig. 1 show the fitting of (4) to the distribution of the duration of short accentuated vowels with Speaker I.

The fitting is very good but not all results were satisfactory.

4. Authors: U.Strauss, G. Altmann

5. References

Geršić, S., Altmann, G. (1988). Ein Modell für die Variabilität der Vokaldauer. Glottometrika 9, 49-58. . (Graph)