Herdan dimension
1. Problem and history
The relation between vocabulary V and text length N (in the number of words) has been many times used as a structural or stylistic characteristic of a text. The problem was discussed by Gustav Herdan (1966: 15) in the following way: ‘... the ratio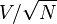 
is of no use since it is obvious that its value changes with sample size, N growing much faster than V. It can therefore not serve as a parameter of the universe of discourse, be the latter a text or a group of texts; the ratio V/N is not much better in this respect. However, the relation log V/log N has proved satisfactory.’
Herdan (1960: 27-28) derived this parameter from the characteristic of text dynamics contained in equations:
dV/dt = βVG
dN/dt = αNG ,
where α, β are specific constants, G measures “environmental” conditions of a text growth and t is time. After elimination of G and integration, equation
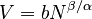
is obtained. With b = 1 and log b = 0, and with C = β/α the resulting equation is
log V = C log N .
For observed texts, in the log-log grid, the relation becomes a line. However, the application of the concept of dimension offers another explanation of the logarithmic transformation of these two sets. This has been mentioned in Hřebíček (2003).
2. Hypothesis:
Parameter logV / logN can be understood as the inverted form of similarity (or fractal) dimension defined on the respective sets.
3. Derivation
The concept of Herdan text dimension can be derived with the help of the intuitive presentation of topological dimension presented by Voss (1988: 28-29). An object of dimension D = 1 consisting of N parts (i. e., a line divided into N equal parts) can be scaled by ratio r = 1/N, so that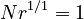 
. For a two-dimensional object, 
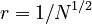and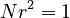 
. For a three-dimensional object, 
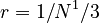and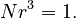 
Etc. Voss presents the following general formula:
(1) 
.
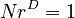As Falconer (1990: 36) stresses, ‘Fundamental to most definitions of dimension is the idea of measurement at scale δ.’ In the case of the cardinal numbers of the two sets discussed, vocabulary and text length, the former is used as a “rule” for measuring the latter. Consequently, the ratio r = 1/V is used as the appropriate scale.
Example: In the first chapter of Jane Austen’s Pride and prejudice the following values were observed: V = 222 and N = 506. When they are substituted to formula (1),
(2)
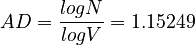
is obtained.
Example: From a poem in the Ottoman language (a ghazel by Mahmud Baki) with N = 60 and V = 42, the value of D = 1.09543 was obtained.
If an arbitrary text contains the respective sets with V = 5 and N = 15, then D = 1.6826. While parameter log V/log N ranges in interval [0; 1], its inverted values belong to interval [1; ∞]. The minimal value of D = 1 corresponds to a text with V = N. The concept of dimension can be imagined as a simple line; if D increases, the line expands into a plain. With D > 2 the dimension expands into a space. The absolute majority of observed texts has D between 1 and 2. This characteristics provides information concerning the internal filling in of the semantic space generated by texts. Using Herdan dimension, different texts even in different languages can be mutually compared. As Voss indicates in the quoted work, relation (2) is usually called similarity or fractal dimension of the respective sets. It is evident that the dynamic and structural-semantic pictures of texts are joined.
4. Author: L. Hřebíček.
5. References
Falconer, G. (1990). Fractal geometry. Mathematical foundations and applications. Chichester – New York: Wiley.
Herdan, G. (1960). Type-token mathematics. The Hague: Mouton.
Herdan, G. (1966). The advanced theory of language as choice and chance. Berlin – Heidelberg – New York: Springer.
Hřebíček, L. (2003). Denotative analysis and Turkish texts. Archiv orientální 71, 187-198.
Voss, R. F. (1988). Fractals in nature: From characterization to simulation. In: Peitgen, H.-O., Saupe, D. (eds). The science of fractal images. New York – Berlin – Heidelberg: Springer.
