Hierarchic relations
1. Problem and history
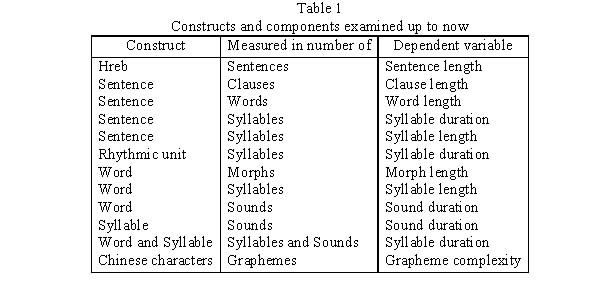
In different domains of language one observed the fact that the length of a construct influences the length of its consitutents. Usually the constituents get smaller with increasing length of the construct but not in all cases. The problem is to find a theoretical model encompassing all dependencies of this kind. The constructs whose length is the independent variable are: hreb, sentence, rhythmic unit, word, syllable; the constituents whose length or duration is the dependent variable are: sentence, clause, word, syllable, morph, sound. There is also the possibility to consider two independent variables, e.g. word (measured in number of syllables) and syllable (measured in number of sounds) , while the dependent variable is the syllable duration. Up to now the following particular cases have been examined (see Table 1)
The origin of the problem can be found in 19th century, in phonetics, probably for the first time with Sievers (1876, 1901) who measured the syllable duration in rhythmic units (Sprechakte). A number of phoneticians tested different hypotheses, a part of which corroborated, another part falsified it. The isochrony hypothesis in English is a special case of this problem. The problem was generalized by Menzerath who stated that the greater the whole the smaller its parts (1954: 101). Different researchers proposed some empirical formulas (Fónagy, Magdics 1960; Nooteboom 1972, 1973; Landblom, Rapp 1972), Altmann (1980) set up the pertinent differential equation and called the result Menzerath´s law. Hřebíček (1992, 1995, 1997) showed that the whole hierarchy of textual levels is based on this dependence and called it Menzerath-Altmann´s law.
There is a great number of individual examinations in different domains of languge. In phonetics the most exhaustive is Weber (1998), in textology the works by Hřebíček (see above) and a mixture of problems including biology and sociology can be found in Altmann, Schwibbe (1989). Bohn (1998) analyzed the relationship between Chinese characters and the complexity of composing graphemes, length of words and simplicity of characters, clause length and word length, sentence length and clause length (cf. also Menzel 2005). The law has a strong corroboration not only within linguistics but displays analogies to other sciences. Thus the simple form of Menzerath´s law is identical with the allometric law in biology and with the power laws current in different sciences. Its correspondences can be found in (i) molecular biology, (ii) sociology of baboons, (iii) in the domain of self-organized criticality, (iv) in chaos research, (v) in the theory of fractals, (vi) in information theory. It has been observed that construct length is not always the only cause of shortening of the constituents. Also accent, vowel quality, syllable structure, frequency etc. can intervene (cf. Weber 1998). In that case more complex formulas must be used. The law has several consequences, all of which must still be tested (cf. Altmann, Schwibbe 1989: 8-14): 1. In longer words more phonetic changes occur than in shorter ones.
2. In languages with greater average word length more phonetic/phonemic changes occur than within the same time interval in languages with smaller average word length
3. The adding of an affix to a word evokes the tendency to reduce the inventory of consonants of the word.
4. The shortening of average syllable length in Hypothesis 3 can also be achieved by inserting epenthetic vowels between the stem and affix (or compounding stem).
5. Partial reduplication is more frequent in natural languages than full reduplication.
6. Short roots/morphemes/stems build more compounds or derived words than long ones.
7. The more elements there are in a compound the shorter they are (see the hypotheses on compounds  )
)
8. Fenk-Fenk (to be inserted)
There are different interpretations of the law:
1. In general, long constructs contain more redundancy than short ones. In order to prevent excessive growth of redundancy one can reduce the size of the constituents. The size, the place and the time of this reduction is not known and cannot be predicted. The analogy to self-organized criticality of sand-piles is evident (cf. Bak 1996).
2. Köhler (1989) shows that mechanism of shortening is a consequence of restrictions of the memory: the longer the construct, the more place must be reserved for the structural information between the constituents, thus the size of the constituents must be reduced.
2. Hypothesis
The size of the components is a function of the construct size.
3. Derivation
The average size of constituents changes with the increase of the size of the construct. It is assumed that the relative rate of change of the size of components is proportional to the rate of change of the size of constructs, the proportionality function being
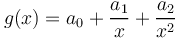 .
.
Thus in case that all other variables other than construct size are subsumed under the ceteris paribus condition one obtains
(1)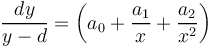 .
.
where d is the minimal value y can attain. In case that there is another independent variable, z, one starts from
(2)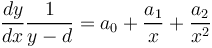 and
and 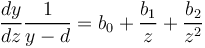
which can be extended to any number of variables. The solution of (1) yields
(3)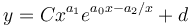
the combining (2) the solution is
(4)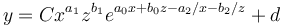
In different applications the following special cases of (3) have been used (d > 0)
(1a) 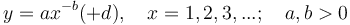
(1b)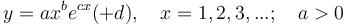
(1c)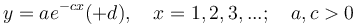
(1d) 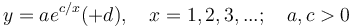
Solution (4) is still very seldom. Both approaches are special cases of the unified theory ( ).
).
Examples:
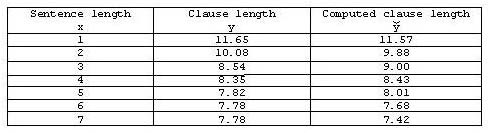
4. Authors: U. Strauss, G. Altmann
5. References
Abercrombie, D. (1967). Elements of general phonetics. Edinburgh: University Press.
Äima, F. (1918). Phonetik und Lautlehre des Inarilappischen. Mémoires de la Societé Finno-Ougrienne 43, 1-249.
Altmann, G. (1980). Prolegomena to Menzerath´s law. Glottometrika 2, 1-10.
Altmann, G. (1983). H. Arens´ „verborgene Ordnung“ und das Menzerathsche Gesetz. In: Faust, M., Harweg, R., Lehfeldt, W. (Hrsg.), Allgemeine Sprachwissenschaft, Sprachtypologie und Textlinguistik: 31-39. Tübingen: Narr.
Altmann, G., Bagheri, D., Goebl, H., Köhler, R., Prün, C. (2002). Einführung in die quantitative Lexikologie. Götingen: Peust & Gutschmidt.
Altmann, G., Beöthy, E., Best, K.-H. (1982). Die Bedeutungskomplexität der Wörter und das Menzerathsche Gesetz. Zeitschrift für Phonetik, Sprachwissenschaft und Kommunikationsforschung 35, 537-543.
Altmann, G., Schwibbe, M. (1989). Das Menzerathsche Gesetz in informationsverarbeitenden Systemen. Hildesheim, Olms.
Arens, H. (1965). Verborgene Ordnung. Düsseldorf: Schwann.
Asleh, L., & Best, K.-H. (2004/05). Zur Überprüfung des Menzerath-Altmann-Gesetzes am Beispiel deutscher (und italienischer) Wörter. Göttinger Beiträge zur Sprachwissenschaft 10/11, 9-19.
Auer, P., Uhmann, S. (1988). Silben- und akzentzählende Sprachen. Zeitschrift für Sprachwissenschaft 7, 214-259.
Bak, P. (1996) How nature works. The science of self-organized criticality. New York: Copernicus-Springer.
Bennett, S.G. (1935). Vergleichende experimentalphonetische Untersuchung der ungespannten Plosive im Englischen, Deutschen und Französischen. Diss.
Bohn, H. (1998). Quantitative Untersuchungen der modernen chinesischen Sprache und Schrift. Hamburg: Kovač.
Bohn, H. (2002). Untersuchungen zur chinesischen Sprache und Schrift. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 127-177. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/
Boroda, M.G., Altmann, G. (1991). Menzerath's law in musical texts. Musikometrika 3, 1-13.
Changizi, M.A. (2001). Universal scaling laws for hierarchical complexity in languages, organisms, bahaviors and other combinatorial systems. J. of Theoretical Biology 211, 277-295.
Collinder, B. (1964). Das Wort als phonetische Einheit. In: Collinder, B. (ed.), Sprachwissenschaft und Wahrscheinlichkeit: 203-217. Uppsala: Almquist, Wiksells.
Cramer, I.M. (2005). The parameters of the Altmann-Menzerath law. J. of Quantitative Linguistics 12(1), 41-52.
Cramer, I.M. (2005a). Das Menzerathsche Gesetz. In: Köhler, R., Altmann, G., Piotrowski, R.G. (eds.), Quantitative Linguistics - An International Handbook: 659-688. Berlin: de Gruyter.
Debowski, L. (2007). Menzerath´s law for the smallest grammar. In: Grzybek, P., Köhler, R. (eds.), Exact methods in the Study of Language and Tests: 77-85. Berlin: de Gruyter.
Donner, K. (1912). Salmin murteen kvantiteettisuehtista. Suomi IV, 9, II.
Elert, C.C. (1965). Phonological studies of quantity in Swedish. Uppsala.
Evertz, (1929). Beiträge zur Phonetik der südfranzösischen Plosive. Diss.
Faure, G., Hirst, D.J., Chafcouloff, M. (1980). Rhythm in English: Isochronism, pitch, and perceived stress. In: Linda, R., Schooneveld, C.H.v. (eds.), The melody of language: 71-79. Baltimore: University Park Press.
Fenk, A., Fenk-Oczlon, G. (1993). Menzerath´s law and the constant flow of linguistic information. In: Köhler, R., Rieger, B.B. (eds.), Contributions to quantitative linguistics: 11-31. Dordrecht: Kluwer.
Fenk-Oczlon, G., Fenk, A. (1995). Selbstorganisation und natürliche Typologie. Sprachtypologie und Universalienforschung 48, 223-238.
Fenk-Oczlon, G., Fenk, A. (1999). Cognition, quantitative linguistics, and systemic typology. Linguistic Typology 3, 151-177.
Fickermann, I., Markner-Jäger, B, Rothe, U. (1984). Wortlänge und Bedeutungskomplexität. Glottometrika 6, 115-126.
Fischer-Jörgensen, E. (1964). Sound duration and place of articulation. Zeitschrift für Phonetik 17, 175-207.
Fónagy, I. (1959). A költöi nyelv hangtanából. Budapest.
Fónagy, I, Magdics, K. (1960). Speed of utterance in phrases of different length. Language and Speech 3, 179-182.
Gaitenby, I.H. (1965). The elastic word. Haskins, Status Report on speech research 1965/SR-2,3.1-3.12.
Gerlach, R. (1982). Zur Überprüfung des Menzerathschen Gesetzes im Bereich der Morphologie. Glottometrika 4, 95-102.
Geršić, S., Altmann, G. (1980). Laut – Silbe – Wort und das Menzerathsche Gesetz. Frankfurter Phonetische Beiträge 3, 115-123.
Grégoire, A. (1899). Variation de la durée de la syllable français. La Parole 1.
Grzybek, P. (1999). Randbemerkungen zur Wortlänge im Kroatischen. In: B.Tošović (ed.), Die grammatischen Korrelationen: 56-67. Graz: Gralis.
Grzybek, P., Stadlober, E. (2007). Do we have probelsm with Arnes´ law? A new look at the sentence-word relation. In: Grzybek, P., Köhler, R. (eds.), Exact Method in th Study of Language and Text: 203-215. Berlin: de Gruyter.
Hammerl, R., Sambor, J. (1993a). O statystycznych prawach jezykowych. Warszawa: Polskie Towarzystwo Semiotyczne.
Hegedüs, L. (1956). Sprechtempoanalysen im Ungarischen. Zeitschrift für Phonetik 10.
Heups, G. (1983). Untersuchungen zum Verhältnis von Satzlänge und Clauselänge am Beispiel deutscher Texte verschiedener Textklassen. Glottometrika 5, 113-133.
Hřebíček, L. (1990). Menzerath-Altmann's law on the semantic level. Glottometrika 11, 47-56.
Hřebíček, L (1990a). The constants of the Menzerath-Altmann law. Glottometrika 12, 61-71.
Hřebíček, L. (1992). Text in communication: Supra-sentence structure. Bochum, Brockmeyer.
Hřebíček, L. (1993b). Text as a construct of aggregations. In: Köhler, R., Rieger, B. (eds.), Contributions to quantitative lingusitics: 33-39. Dordrecht: Kluwer.
Hřebíček, L. (1993c). Text as a strategic process. In: Hřebíček, L., Altmann, G. (Eds.), Quantitative text analysis: 136-150. Trier: WVT.
Hřebíček, L. (1994). Fractals in language. J. of Quantitative Linguistics 1, 82-86.
Hřebíček, L. (1994a). The stairway of subsystems. In: 2nd International Conference on Quantitative Linguistics, September 1994, 210-222 Moscow. Moscow: Lomonosov Moscow State University.
Hřebíček, L. (1995). Text levels. Language constructs, constituents and Menzerath-Altmann law. Trier: WVT.
Hřebíček, L. (1995a). Phase transition in texts. ZeT – Zeitschrift für empirische Textwissenschaft 2, 52-58.
Hřebíček, L. (1997). Lectures on text theory. Prague: Oriental Institute.
Hřebíček, L. (2000). Variation in sequences. Prague: Oriental Institute.
Hřebíček, L. (2004). The semantic space and Turkish ghazels. Archiv orientální 72, 175-191.
Hřebíček, L. (2005). Text laws. In: Köhler, R., Altmann, G., Piotrowski, R.G. (eds.) (2005), Quantitative Linguistics - An International Handbook: 348-361. Berlin: de Gruyter.
Hřebíček, L., Altmann, G. (1993). Prospects of text linguistics. In: Hřebíček, L., Altmann, G. (Eds.), Quantitative text analysis: 1-28. Trier: WVT.
Hug, M. (2007). Das Menzerath-Gesetz in der Vulgata. In: Grzybek, P., Köhler, R. (eds.), Exact Method in th Study of Language and Text: 243-255. Berlin: de Gruyter.
Huxley, A. (1963). Evolution: the modern synthesis. London 1942.
Jespersen, O. (1897-1899). Phonetik. Copenhagen.
Jespersen, O. (1932). Lehrbuch der Phonetik. Lepzig-Berlin.
Kaumanns, W., Schwibbe, M.H. (1983). Strukturmerkmale von Primatensozietäten unter dem Gesichtspunkt der Menzerathschen Regel. In: Altmann, G., Schwibbe, M. (1983): 99-107.
Köhler, R. (1982). Das Menzerathsche Gesetz auf der Satzebene. Glottometrika 4, 103-113.
Köhler, R. (1984). Zur Interpretation des Menzerathschen Gesetzes. Glottometrika 6, 177-183.
Köhler, R. (1986). Zur linguistischen Synergetik: Struktur und Dynamik der Lexik. Bochum: Brockmeyer.
Köhler, R. (1989). Das Menzerathschen Gesetz als Resultat des Sprachverarbeitungsmechanismus. In: Altmann, Schwibbe (1989): 108-112.
Köhler, R. (1990). Linguistische Analyseebenen, Hierarchisierung und Erklärung im Modell der sprachlichen Selbstregulation. Glottometrika 11, 1-18.
Krott, A. (1996). Some remarks on the relation between word length and morpheme length. J. of Quantitative Linguistics 3, 29-37.
Krott, A. (2002). Ein funktionalanalytisches Modell der Wortbildung. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 75-126. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/
Kułacka, A., Mačutek, J. (2007). A discrete formula for the Menzerath-Altmann law. J. of Quantitative Linguistics 14(1), 23-32.
Laurosela, J. (1922). Foneettinen tutkimus Etelä-Pohjanmaan murteesta. Helsinki.
Lehiste, I. (1970). Suprasegmentals. Cambridge, Mass.:M.I.T. Press.
Lehfeldt, W. (2006). The fall of jers in the light of Menzerath´s law. In: Grzybek, P. (ed.), Contributions to the Science of text and Language. Word Length and Related Issues: 211-213. Dordrecht: Springer.
Lehfeldt, W., Altmann, G. (2000). Padenie reducirovannykh v svete zakona P. Mencerata. Russian Linguistics 26, 327-344.
Lehfeldt, W., Altmann, G. (2000). Der altrussische Jerwandel. Glottometrics 2, 34-44.
Lehtonen, J. (1970). Aspects of quantity in a standard Finnish. Studia Philologica Jyväskyläensia 6.
Leopold, E. (2001). Fractal structures in language. The question of the imbedding space. In Uhlířová, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a linguistic paradigm: levels, constituents, constructs. Festschrift in honour of Ludek Hřebíček: 163-1176. Trier: WVT.
Leopold, E. (2007). Bemerkungen zum Menzerath-Altmannschen Gesetz. In: Grzybek, P., Köhler, R. (eds.), Exact Methods in the Study of Language and Text: 389-396. Berlin: de Gruyter.
Lindblom, B.E.F. (1968). Temporal organization of syllable production. Royal Institute of Technology, Stockholm, Speech Transmission Laboratory, Quarterly Progress and Status Report 2-3, 1-5.
Lindblom, B, Rapp, K. (1972). Reexamination of the compensatory adjustment of vowel duration in Swedish words. Symposium on experimental and theoretical approaches to the role of time speech. University of Essex.
Maack, A. (1949). Die spezifische Lautdauer deutscher Sonanten. Zeitschrift für Phonetik 3, 190-232.
Malécot, A., Johnston, R., Kizziar, P.-A. (1972). Syllabic Rate and Utterance Length in French. Phonetica 26, 235-251.
Malmberg, B. (1944). Die Quantität als phonetisch-phonologischer Begriff. Lunds Universitets Årskrift 41, 1-104.
Menzerath, P. (1928). Über einige phonetische Probleme. Actes du premier congrès international de linguistique. Leiden, Nendeln/Liechtenstein, Kraus reprint: 104-105.
Menzerath P. (1954). Die Architektonik des deutschen Wortschatzes. Bonn, Dümmler.
Meyer, E.A. (1904). Zur Vokaldauer im Deutschen. Nordiska Studier Tillegnade A: 347-356. Norken, Uppsala 1904.
Meyer, E.A., Gombocz, Z. (1908). Zur Phonetik der ungarischen Sprache. Le Monde Oriental 2, 122-187.
Meyer, P. (2007). Two semi-mathematical asides on Menzerath-Altmann´s law. In: Grzybek, P., Köhler, R. (eds.), Exact Methods in the Study of Language and Text: 447-458. Berlin: de Gruyter.
Nemcová, E. (1994). On two realizations of Menzerath´s law. J. of Quantitative Linguistics 1, 107-112.
Nooteboom, S.G. (1972a). The interaction of some intra-syllable and extra-syllable factors acting on syllable nucleus duration. IPO Annual Progress report 7, 30-39.
Nooteboom, S.G. (1972b). Production and perception of vowel duration. Eindhoven: Philips Research Laboratories.
Nooteboom, S.G. (1973). The perceptual reality of some prosodic durations. J. of Phonetiocs 1, 25-45.
Palomaa, J.K. (1946). Suomen kielen äännekestoista puhumaan oppinen kuuromykän ja kuulevan henkilön ääntämisessä. Publicationes Instituti Phonetici Universiatis Helsingforsiensis. Turku.
Polikarpov, A. (2000). Menzerath’s Law for Morphemic Structures of Words: A Hypothesis for the Evolutionary Mechanism of its Arising and its Testing. In: Baayen, R.H. (ed.), Proceedings of the fourth conference of the International Quantitative Linguistics Association: 26-27, Prague, August 24-26, 2000.
Polikarpov, A.A. (2006). Towards the foundations of Menzerath´s law. On the functional dependence of the affix lengths on their positional number within words. In: Grzybek, P. (ed.) Contributions to the Science of Text and Language. Word Length Studies and Related Issues: 215-240. Dordrecht: Springer.
Prün, C. (1994). Validity of Menzerath-Altmann’s law: Graphic representation of language, information processing systems and synergetic linguistics. J. of Quantitative Linguistics 1, 148-155.
Rothe, U. (1983). Wortlänge und Bedeutungsmenge. Eine Untersuchung zum Menzerathschen Gesetz an drei romanischen Sprachen. Glottometrika 5, 101-112.
Roudet, L. (1910). Eléments de phonétique générale. Paris: Welter.
Ruszkowski, M. (1991). Prawo Menzeratha w badaniach syntaktycznych. Jezyk Polski LXXI, 187-192.
Rykov, V. (1994). Menzerath law for printed speech. In: 2nd International Conference on Quantitative Linguistics, September 20-24, 1994, Moscow: 199-200. Moscow: Lomonosov Moscow State University.
Sambor, J. (1984). Menzerath’s law and the polysemy of words. Glottometrika 6, 94-114.
Schindelin, C. (2005). Die quantitative Erforschung der chinesischen Sprache und Schrift. In: Köhler, R., Altmann, G., Piotrowski, R.G. (eds.), Quantitative Linguistics - An International Handbook: 947-970. Berlin: de Gruyter.
Schwibbe, M.H. (1984). Text- und wortstatistische Untersuchungen zur Validität der Menzerathschen Regel. Glottometrika 6, 152-176.
Schwibbe, M.H. (1989). Die Menzerathsche Regel als Modell psychischer Informationsverarbeitung. In: Altmann, G., Schwibbe, M.H. (1989): 84-91.
Sievers, E. (1876/1901). Grundzüge der Phonetik. Leipzig: Breitkopf, Härtel.
Sovijärvi, A. (1944). Foneettis-äännehistoriallinen tutkimus Soikkolan inkeroismurteesta. Suomi 103.
Tarnóczy, T. (1965). Can the problem of automatic speech recognition be solved by analysis alone? Reports of the Fifth International Congress of Acoustics II, Liège.
Teupenhayn, R., Altmann, G. (1984). Clause length and Menzerath´s law. Glottometrika 6, 127-138.
Weber, S. (1998). Das Menzerathsche Gesetz in gesprochener Sprache. Magisterarbeit Universität Trier.
Wiik, K. (1965). Finnish and English vowels. Turku, Annales Universitatis Turkuensis, Series B, 94.
Wilde, J., Schwibbe, M.H. (1989). Einige methodologische Überlegungen zur Menzerathschen Regel. In: Altmann, Schwibbe 1989: 113-116.
Wilde, J., Schwibbe, M.H. (1989a). Organisationsformen von Erbinformation im Hinblick auf die Menzerathsche Regel. In: Altmann, Schwibbe 1989: 92-99.
Wimmer, G., Altmann, G. (2005). Unified derivation of some linguistic laws. In: P. Grzybek (ed.), Contributions the the Science of Language. Word Length Studies and Related Issues: 329-337. Dordrecht: Kluwer.
Ziegler, A., Altmann, G. (2002). Denotative Textanalyse. Wien: Edition Praesens.
The allometric law in other sciences
Adolph, E.F. (1949). Quantitative relations in physiological constitution of mammals. Science 109, 579-
Bertalanffy, L.v. (1949). Problems of organic growth. Nature 163, 156-
Bertalanffy, L.v. (1951). Theoretische Biologie. Vol. II, Stoffwechsel, Wachstum. 2nd ed. Bern:
Bertalanffy, L.v. (1951a). Growth types and metabolic types. American Naturalist 85, 111-
Bertalanffy, L.v., Pirozynski, W.J. (1952). Ontogenetic and evolutionary allometry. Evolution 6, 3287-.
Bertalanffy, L.v., Pirozynski, W.J. (1953). Tissue respiration, growth and basal metabolism. Biological Bulletin 105, 240-.
Bonin, G.v. (1937). Brain weight and body weight of mammals. J. of General Psychology 16,
Brody, S. (1945). Bioenergetics and growth. New York:
Hersh, A.H. (1941). Allometric growth: The ontogenetic and phylogenetic significance of differential rates of growth. 3rd Growth Symposium 113.
Huxley, J. (1932). Problems of relative growth. London.
Jerison, H.J. (1955). Brain to body ratios and the evolution of intelligence. Science 121, 477-
Kaumanns, W., Schwibbe, M.H. (1989). Strukturmerkmale von Primatensozietäten unter dem Gesichtspunkt der Menzerathschen Regel. In: Altmann, G., Schwibbe, M.H., Das Menzerathsche Gesetz in informationsverarbeitenden Systemen: 99-107. Hildesheim: Olms.
Klatt, B. (1919). Zur Methodik vergleichender metrischer Untersuchungen, besonders des Herzgewichts. Biologisches Zentralblatt 39, 406-
Naroll, R.S., Bertalanffy, L.v. (1956). The principle of allometry in biology and the social science. General Systems 1, 76-89.
Needham, J. (1934). Chemical heterogony and the groundplan of animal growth. Biological Revue 9, 79-.
Reed, W.J., Hughes, B.D. (2002). From gene families and genera to incomes and internet file sizes: why power laws are so common in nature. Physical Review E 66, 067103.
Reeve, E.C.R., Huxley, J.S. (1945). Some problems in the study of allometric growth. In: Clark, W.E.C., Medawar, P.B. (1945), Essays on growth and form, presented to D´Arcy Wentworth Thmpson: 121-. Oxford:
Rensch, B. (1954). Neuere Probleme der Abstammungslehre. 2nd ed. Stuttgart:
Robb, R.C. (1935-1937). A study of mutation in evolution. I-IV. J. of Genetics 31, 39-; 33, 269-; 34, 477-.
Sholl, D.A. (1954). Regularities in growth curves, including rhythms and allometry. In: Boell, E.J. (ed.), Dynamics of growth processes: 224-. Princeton:
Vining, R. (1955). A description of certain spatial aspects of an economic system. Economic Development and Culture Change 3, 147-.