Hreb length
1. Problem and history
Up to now two kinds of “hrebs” have been established:
Sentence hreb is a set of sentences of the text containing the same word, the same denotation or the same reference. Hřebíček calls them “(sentence) aggregates” or “larger contexts”.
Denotation hreb is a set of elements of a text having the same denotation. There can be word hrebs, considering merely the denotation of words, morpheme hrebs, considering the reference of all morphemes, or phrase hrebs.
The criteria for establishing hrebs are not yet unique.
The discoverer of these units is Hřebíček (1990, 1992, 1993, 1995, 1995a, 1997) who examined their length especially in Turkish texts and used exclusively the Zipf-Alekseev distribution. Schwarz (1995) extended the research to German texts and used also the Waring distribution. Ziegler and Altmann (2002) developed some theoretical issues concerning denotation hrebs and in fact baptized these entities “hrebs”.
2. Hypothesis
Hreb length abides by the usual length distribution following from the unified theory ( ) or the Zipf-Alekseev distribution used in word association research (
) or the Zipf-Alekseev distribution used in word association research ( ).
).
3. Derivation
In the usual “length”-approach, 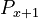 =
= 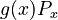 , one inserts
, one inserts 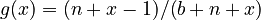 and obtains the 1-displaced version of the Waring distribution
and obtains the 1-displaced version of the Waring distribution
(1) 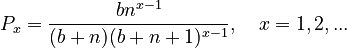
For the derivation of the Zipf-Alekseev distribution see “Word associations” ( ).
).
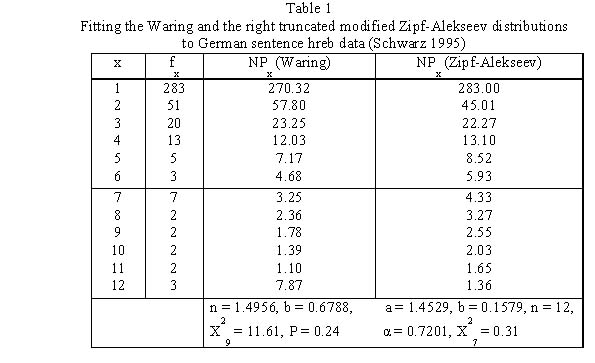
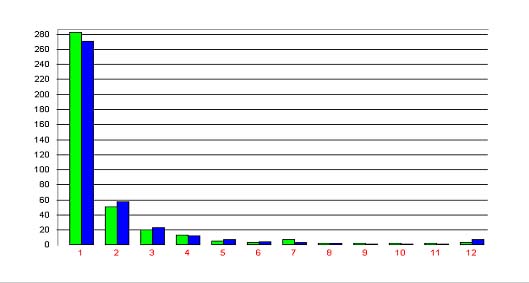
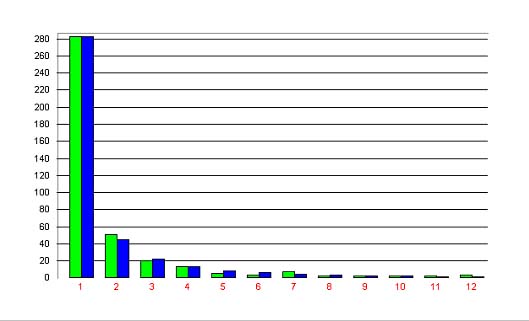
Example. Sentence hreb length in a German text (Schwarz 1995)
Schwarz analyzed a German text (F. Schirmacher, “Dem Druck des härteren, strengeren Lebens standhalten.“ Frankfurter Allgemeine Zeitung 2.6.1990, Nr. 127) and obtained the results in Table 1 and Figures 1 and 2.
In this case, the Zipf-Alekseev distribution yields sowhat better results, in spite of the fact that it has 4 paramaters. However, bothe fittings are satisfactory.
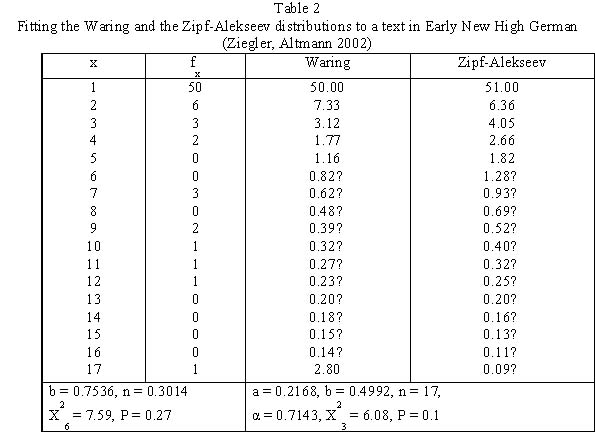
Example: Denotation hreb length in an Early New High German text (Ziegler, Altmann 2002).
Ziegler and Altmann examined a letter form an Archive in Bratislava written in Early New High German segmented to denotation hrebs. The results are given in Table 2. This time the Waring distribution is slightly better.
4. Authors:U. Strauss, G. Altmann
5. References:
Hřebíček, L. (1992). Text in communication: Supra-sentence structure. Bochum, Brockmeyer.
Hřebíček, L. (1993a). Text as a construct of aggregations. In: Köhler, R., Rieger, B. (eds.), Contributions to quantitative linguistics. Dordrecht: Kluwer: 33-39.
Hřebíček, L. (1995). Text levels. Language constructs, constituents and Menzerath-Altmann law. Trier: WVT.
Hřebíček, L. (1996). Word associations and text. Glottometrika 15, 12-17.
Hřebíček, L. (1997). Lectures on text theory. Prague: Oriental Institute.
Schwarz, C. (1995). The distribution of aggregates in texts. ZeT – Zeitschrift für empirische Textforschung 2, 62-66
Ziegler, A., Altmann, G. (2002). Denotative Textanalyse. Wien: Edition Praesens.
Uhlirova 2003; (Rez.), Lehfeldt 2003 (Rez.), Andersen 2003 Rez.; Grzybek 2003 Rez.; (Ergänzen später)