Morphological productivity
1. Problem and history
In the lexicon of a language there are two processes working:
(a) Birth of new lexemes by creating or borrowing
(b) Death by elimination of lexemes
Birth means either creation of new words or constructing them by morphological processes like derivation, reduplication, compounding etc. The construction is a case of (multidi-mensional) diversification ( ). At the same time it is a case of specification of meaning and word prolongation. Birth and death take place in rates called birth-rate
). At the same time it is a case of specification of meaning and word prolongation. Birth and death take place in rates called birth-rate 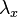 and death-rate
and death-rate 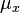 respectively.
Since up to now only a case of derivation has been examined, the hypothesis must be restricted but we assume that it holds for other kinds of word building, too. It holds, of course, only under the condition that the given way of word buidling is actual in a language.
As far as known, the only model was proposed by Wimmer and Altmann (1995) in which the random variable x is the number of derivates built from a stem (x = 0,1,2,…) and
respectively.
Since up to now only a case of derivation has been examined, the hypothesis must be restricted but we assume that it holds for other kinds of word building, too. It holds, of course, only under the condition that the given way of word buidling is actual in a language.
As far as known, the only model was proposed by Wimmer and Altmann (1995) in which the random variable x is the number of derivates built from a stem (x = 0,1,2,…) and 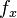 is the number of stems having x derivates.
is the number of stems having x derivates.
2. Hypothesis
Morphological productivity is the result of a birth-and-death process in which stems build new derivates and some derivates are eliminated. The probability of the number of stems having x derivates follows the Pólya distribution.
3. Derivation
The creation of new morphological constructs is proportional to the class size x and can be generally symbolized as a + cx. Since creation cannot be infinite, there must be a limit n to it. The community controls the creation in the same linear way symbolized as b + (n-x-1)c. This results in the birth rate 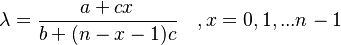 . The death rate is similar, depending only on the class size and the morphological nature of language. It can be sym-bolized as
. The death rate is similar, depending only on the class size and the morphological nature of language. It can be sym-bolized as 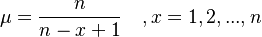 Inserting the above birth-rate and death-rate in the balancing birth-and-death equations and reparametrizing
Inserting the above birth-rate and death-rate in the balancing birth-and-death equations and reparametrizing
p = a/(a+b), q = b/(a+b), s = c/(a+b)
we obtain the Pólya distribution (Wimmer, Altmann 1995)
(1)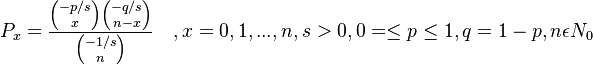
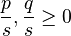 or
or 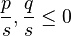
Example: Indonesian stem productivity
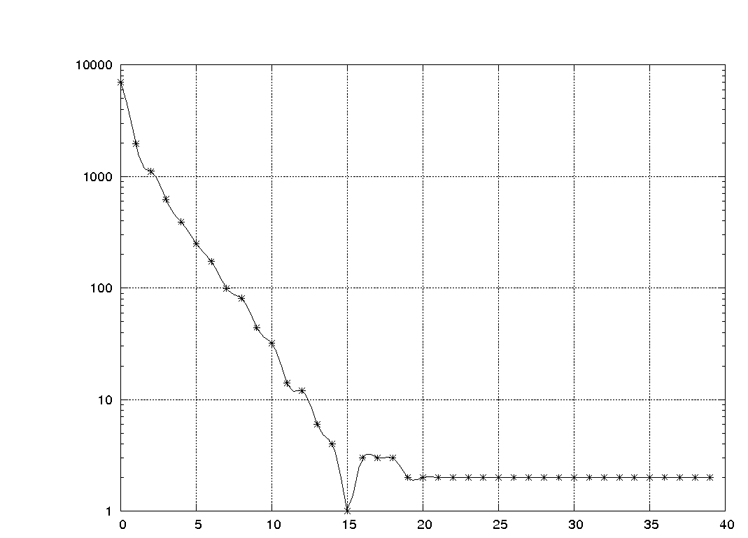
Wimmer and Altmann (1995) studied the productivity of stems in the Indonesian dictionary (Echols, Shadily 1963). There were 6970 stems having no derivates, 1961 stems having each 1 derivate etc. The data and the results of fitting are presented in Table 1 and Fig. 1.
4. Authors: U. Strauss, G. Altmann
5. References
Altmann, G., Bagheri, D., Goebl, H., Köhler, R., Prün, C. (2002). Einführung in die quantitative Lexikologie. Götingen: Peust & Gutschmidt.
Echols, J.M., Shadily, H. (1963). An Indonesian-English dictionary. Ithaca: Cornell University Press.
Wimmer, G., Altmann, G. (1995). A model of morphological productivity. J. of Quantitative Linguistics 2, 212-216.