Sentence and clause length
1. Problem and history
The problem is to find the distribution of sentence and/or clause length in texts. To this end two previous problems must be solved or operationalized:
(i) The determination of sentence boundaries (cf. esp. Niehaus 2001) which is extremely difficult in speech but feasible in written texts. Usually it is achieved with the aid of numerous criteria which can differ from language to language.
(ii) The determination of the measurement unit. One obtains different models for different measurement units, e.g. clauses or words or syllables or phonemes. Today merely the first two are used, sometimes in modified form. Several hundreds of tests in different languages performed in the framework of Göttingen Project corroborate this kind of modelling (Altmann 1988b; Best 2001a,b, 2003, 2006; Grzybek 1995, 1999, 2001; Jing 2001; Kaßel, Livesey 2001; Niehaus 1997, 2001; Rheinländer 2000; Rottmann 2001; Roukk 2001, 2001a; Strehlow 1997; Uhlířová 2001; Wittek 2001).
Historically, the first who tackled the problem was Sherman (1888) using sentence length for characterization purposes. Altmann (1988b) baptized these laws to Sherman´s laws. Older empirical data were collected especially in Classical Greek, in English, Russian and Slovak (Marckworth, Bell 1967; Martynenko 1965; Mistrík 1967; Morton 1965; Morton, Levison 1966; Morton, McLeman 1966; Clayman 1981). Modelling goes back to Yule (1939, 1944), Williams (1940, 1970), Lesskis (1962), Martynenko (1965), Fucks (1955; 1970/71), Buch (1969), Sichel (1974); today it is part of the unified theory ( ), the first models in this direction were set up by Altmann (1988b).
), the first models in this direction were set up by Altmann (1988b).
2. Hypothesis
Sentence and clause lengths in texts abide by regular probability distributions derived from the unified theory ( ).
).
3. Derivation (Altmann 1988b)
The speaker (writer) tends to prolong the actual length of the sentence x adding further clauses, affecting it linearly in the form a + bx. The consideration for the hearer (reader) brakes this trend with force cx. Thus, if sentence length is measured in the number of clauses, one obtains
(1)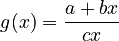 .
.
Inserting g(x) as a proportionality function in (10) esp. Example 6 of Unified Theory (à) and reparametrizing, one obtains the negative binomial distribution
(2)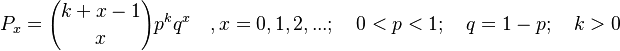 .
.
Some authors define sentence as having at least one clause even if there is no finite verb in it. In that case, one solves the pertinent difference equation for x = 1, 2,... and obtains the positive negative binomial distribution
(3)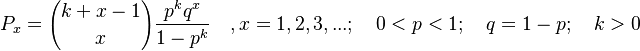 . .
. .
Example: Sentence length in clauses
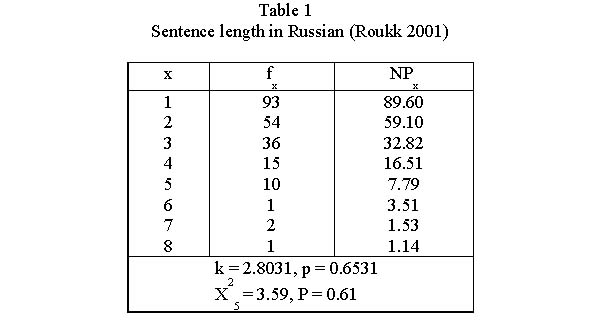
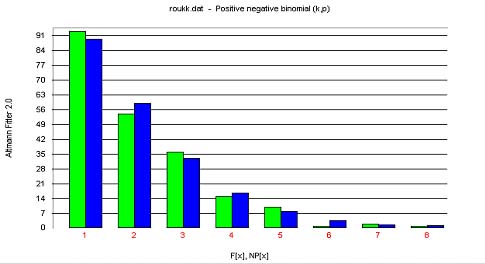
Roukk (2001) measured the sentence length (in clauses) in Čechov´s stories and fitted the positive negative binomial distribution as given in Table 1 and Fig. 1.
Example: Length of clauses in Bulgarian
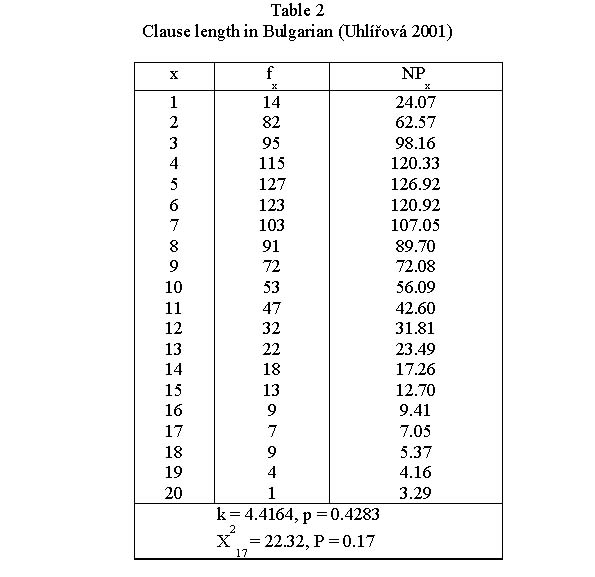
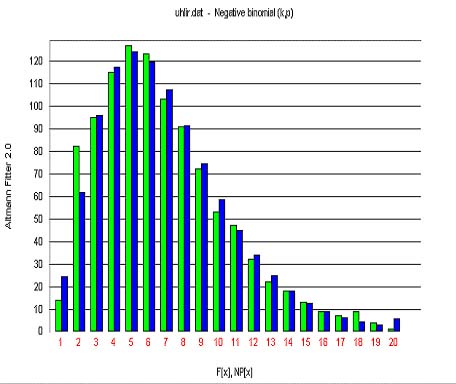
Uhlířová (2001) measured the length of clauses in a collection of letters of a Bulgarian native speaker and obtained the results in Table 2, Fig. 2.
If the measurement unit is word, then there is an intermediate level exerting a constant effect d added to cx, i.e. one obtains
(4)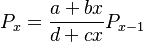 ,
,
yielding, after reparametrization, the hyperpascal distribution
(5)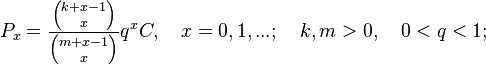
C being the normalizing constant,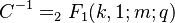 .
.
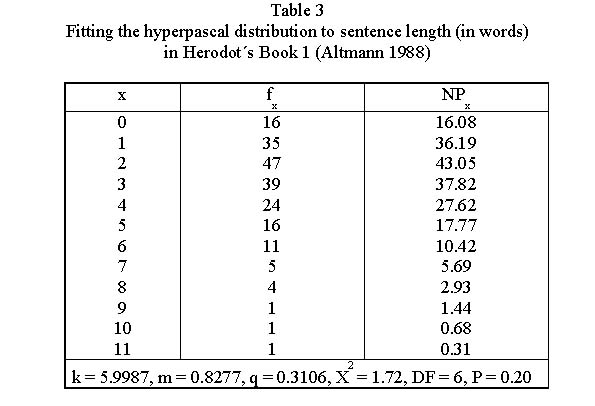
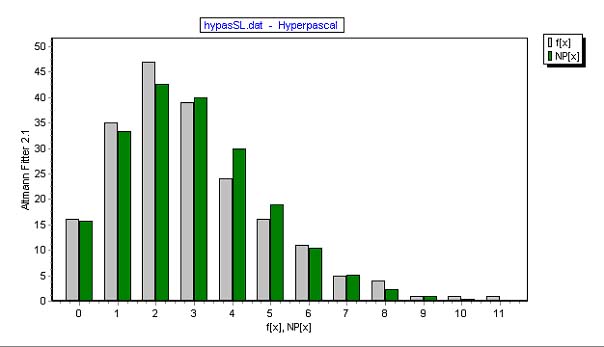
Example. Sentence length in Herodot´s Book 1
Altmann (1988) has shown that under this condition the sentence length follows the hyperpascal distribution using 244 texts. The fitting of (5) to Herodot´s Book 1 is shown in Table 3 and Fig. 3.
Under favourable boundary conditions, one can use all special or limiting cases of these distributions (cf. Wimmer, Altmann 1999).
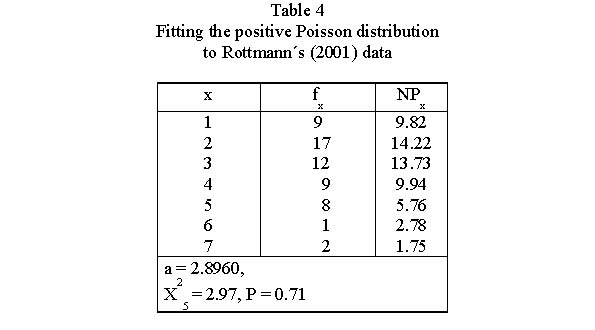
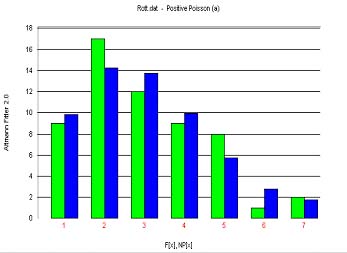
Example: Sentence length in Old Church Slavonic using the positive Poisson distribution For Old Church Slavonic texts, Rottmann (2001) and for German texts Wittek (2001) use the positive Poisson distribution which is the limiting case of the positive negative binomial distribution
(6)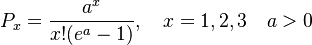 .
.
Example: Modified positive Poisson distribution for German texts
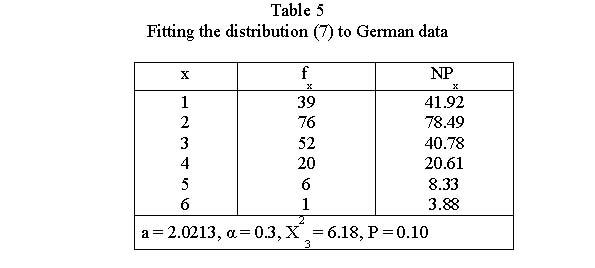
Wittek (2001) obtained good results for 80 German texts using the positive Poisson distribution. However, in 4 cases he was forced to modify the first two classes of the positive Poisson distribution and obtained
(7)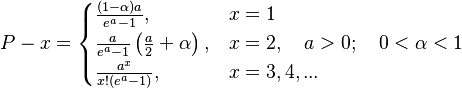
The results of fitting are shown in Table 5.
Uhlířová (2001) used for Bulgarian clauses the mixed negative binomial distribution, but it can be shown that the usual negative binomial distribution is sufficient.
4. Authors: U. Strauss, G. Altmann, K.-H. Best
5. References
Admoni, Wladimir (1973). Die Entwicklungstendenzen des deutschen Satzbaus von heute. München: Hueber.
Altmann, G. (1988a). Wiederholungen in Texten. Bochum, Brockmeyer.
Altmann, G. (1988b). Verteilungen von Satzlängen. Glottometrika 9, 147-170.
Altmann, G. (1992). Sherman´s laws of sentence length distribution. In: Saukkonen, P. (ed.), What is Language Synergetics?: 38-39. Oulu: University of Oulu.
Bartkowiakowa, A. (1963). O rozkładzie i kolejności zdań współrzędnych i podrzędnych w utworach powieściowych żeromskiego i Sienkiewicza. Zastosowania matematyki, Tom VII, 133-154.
Best, K.-H. (2001a). Wie viele Wörter enthalten Sätze im Deutschen? Ein Beitrag zu den Shermann-Altmann-Gesetzen. In: Best, K.-H. (ed.), Häufigkeitsverteilungen in Texten: 167-201. Göttingen: Peust & Gutschmidt.
Best, K.-H. (2001b). Satzlängen im Deutschen: Verteilungen, Mittelwerte, Sprachwandel. Göttinger Beiträge zur Sprachwissenschaft 7, 7-31.
Best, K.-H. (2001c). Probability distributions of language entities. J. of Quantitative Linguistics 8, 1-11.
Best, K.-H. (2002). Satzlängen im Deutschen: Verteilungen, Mittelwerte, Sprachwandel. Göttinger Beiträge zur Sprachwissenschaft 7, 7-31.
Best, K.-H. (2003). Quantitative Linguistik. Eine Annäherung. 2., überarb. u. erw. Aufl. Göttingen: Peust & Gutschmidt. (3. Aufl. in Vorbereitung)
Best, K.-H. (2005). Satzlänge. In: Altmann, G., Köhler, R., Piotrowski, R. (eds.), Quantitative Linguistik - Quantitative Linguistics. Ein internationales Handbuch: 298-304. Berlin/ N.Y.: de Gruyter.
Best, K.-H. (2006). Quantitative Untersuchungen zum Niederdeutschen und Niederländischen. Göttinger Beiträge zur Sprachwissenschaft 13, 51-71.
Best, K.-H. (2006). Verteilung von Phrasen- und Subsatzlängen in deutscher Fachsprache. Naukovyj Visnyk Černivec’koho Universytetu: Hermans’ka filolohija. Vypusk 319-320, 113-120.
Bohn, H. (1998). Quantitative Untersuchungen der modernen chinesischen Sprache und Schrift. Hamburg: Kovač.
Buch, K.R. (1969). A note on sentence-length as random variable. In: Doležel, L., Bailey, R.W. (eds.), Statistics and Style: 76-79. New York: Elsevier.
Busch, A. (2002). Zur Entwicklung der Satzlängen in deutscher Fachsprache. Staatsexamensarbeit, Göttingen.
Clayman, D.L. (1981). Sentence length in Greek hexameter poetry. In: Grotjahn, R. (ed.), Hexameter Studies: 107-136. Bochum: Brockmeyer.
Dshurjuk, T.V., Levickij, V.V. (2003). Satztypen und Satzlängen im Funktional- und Autorenstil. Glottometrics 6, 40-51.
Eggers, Hans (1962). Zur Syntax der deutschen Sprache der Gegenwart. Studium Generale 15, 49-59.
Eggers, Hans (1967). Beobachtungen zur Häufigkeit deutscher Wortformen. Wirkendes Wort 17, 93-105.
Eggers, Hans (1973). Deutsche Sprache im 20. Jahrhundert. München: Pieper.
Fan Fengxiang (2007). A corpus based quantitative study on the change of TTR, word length and sentence length of the English language. In: Grzybek, P., Köhler, R. (eds.), Exact methods in the Study of Language and Texts: 123-130. Berlin: de Gruyter
Fenk-Oczlon, G., Fenk, A. (1985). The mean length of propositions is seven plus minus two syllables – but the position of languages within this range is not accidental. In: d’Ydewalle, G. (ed.), Cognition, Information Processing, and Motivation: 355-359. Amsterdam: Elsevier.
Fontański, H. (1972). Ponjatija i metody matematičeskoj statistiki i teorii verojatnostej, primenjaemye pri issledovanii rozmerov predloženij. Zeszyty naukowe Wyższej Szkoly Pedagogicznej w Opolu 1972/9, 41-51.
Fucks, W. (1955). Mathematische Analyse von Sprachelementen, Sprachstil und Sprachen. Köln – Opladen: Westdeutscher Verlag.
Fucks, W. (1956). Die mathematischen gesetze der Bildung von Sprachelementen aus ihren Bestandteilen. Nachrichtentechnische Forschungsberichte 3, 7-21.
Fucks, W. (1968). Nach allen Regeln der Kunst. Stuttgart: Deutsche Verlags-Anstalt.
Fucks, W. (1970/71). Über den Gesetzesbegriff einer exakten Literaturwissenschaft, erläutert an Sätzen und Satzfolgen. Zeitschrift für Literaturwissenschaft und Linguistik 1, 113-137.
Grzybek, P. (1995). Zur Frage der Satzlänge von Sprichwörtern (unter besonderer Berücksichtigung deutscher Sprichwörter). In: Baur, R, Chlosta, Ch. (Hrsg.), Von der Einwort-metapher zur Satzmetapher. Akten des Westfälischen Arbeitskreises „Phraseologie/ Päromiologie (1994/95)“. Bochum: Brockmeyer.
Grzybek, P. (1999). Wie lang sind slowenische Sprichwörter? Anzeiger für Slavische Philologie XXVII, 87-108.
Grzybek, P. (2000). Pogostnostna analiza besed iz elektronskego korpusa slovenskih besedil. Slavistična Revija Apr.-jun. 2000, 141-157.
Grzybek, P. (2001). Zur Satz- und Teilsatzlänge zweigliedriger formeller Sprichwörter. In Uhlířova, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a Linguistic Paradigm: Levels, Constituents, Constructs. Festschrift in Honour of Ludek Hřebíček: 64-75. Trier: WVT.
Hřebíček, L. (1992). Text in Communication: Supra-sentence Structure. Bochum, Brockmeyer.
Hřebíček, L. (1995). Text Levels. Language Constructs, Constituents and Menzerath-Altmann Law. Trier: WVT.
Hřebíček, L. (1997). Lectures on Text Theory. Prague: Oriental Institute.
Hug, M. (2001). Wort- und Satzlänge als parallele stilistische Parameter. Kontexte der französischen Demonstrativpronomina celui-ci und celui-là. In Uhlířová, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a Linguistic Paradigm: Levels, Constituents, Constructs. Festschrift in Honour of Ludek Hřebíček: 98-107. Trier: WVT.
Ivanov, V.I., Ivanova, T.S. (1978). O razmerach predloženija v sovremennoj čuvašskoj i nemeckoj chudožestvennoj proze. Sopostavitel´naja lingvistika i obučenie inostrannym jazykam v uslovijach dvujazyčija 3, 48-74 (Čeboksary).
Janson, T. (1964). The problem of measuring sentence-length in classical texts. Studia Linguistica 18, 26-36.
Jing, Z. (2001). Satzlängenhäufigkeiten in chinesischen Texten. In: Best, K.-H. (ed.), Häufigkeitsverteilungen in Texten: 202-210. Göttingen: Peust & Gutschmidt.
Kaßel, A., Livesey, E. (2001). Untersuchungen zur Satzlängenhäufigkeit im Englischen: Am Beispiel von Texten aus Presse und Literatur (Belletristik). Glottometrics 1, 27-50.
Kelih, E. (2002). Untersuchungen zur Satzlänge in slowenischen und russischen Prosatexten. Graz: Diss.
Kelih, E., & Grzybek, P. (2004). Häufigkeiten von Satzlängen: Zum Faktor der Intervallgröße als Einflussvariable (am Beispiel slowenischer Texte). Glottometrics 8, 23-41.
Kučera, H., Francis, W.N. (1967). Computational Analysis of Present-day American English. Providence: Brown University Press.
Lauter, J. (1966). Untersuchungen zur Sprache von Kants “Kritik der reinen Vernunft”. Köln: Westdeutscher Verlag.
Lesskis, G.A. (1962). O razmerach predloženij v russkoj naučnoj i chudožestvennoj proze 60-ch godov XIX veka. Voprosy jazykoznanija 12, Nr. 2, 78-95.
Lesskis, G.A. (1963). O zavisimosti meždu razmerom predloženija i charakterom teksta. Voprosy jazykoznanija 3, 92-112.
Lesskis, G.A. (1964). O zavisimosti meždu razmerom predloženija i ego strukturoj v raznych vidach teksta. Voprosy jazykoznanija 13, Nr.3,99-123.
Levickij, V.V., Pavlyčko, O.O., Semenyuk, T.G. (2001). Sentence length and sentence structure as statistical characteristics of style in prose. In: Uhlířová, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a Linguistic Paradigm: Levels, Constituents, Constructs. Festschrift in Honour of Ludek Hřebíček: 177-186. Trier: WVT.
Levison, M., Morton, A.Q., Winspear, A.D. (1968). The seventh letter of Plato. Mind 77, 209-325.
Livesey, E. (2001). Satzlängen im Deutschen und Englischen. Staatsexamensarbeit, Göttingen.
Lua, Kim Teng (1993). The number of syllables in a Chinese sentence. Computer Processing of Chinese and Orietal Languages 7(3), 167-190.
Marckworth, M.L., Bell, L.M. (1967). Sentence-length distribution in the corpus. In: Kučera, H., Francis, W.N. (1967). Computational Analysis of Present-day American English: 374-376. Providence: Brown University Press.
Mistrík, J. (1967). Dĺžka vety pri štylistickej charakteristike. Slovenská reč 32, 19-25.
Morton, A.Q. (1965). The authorship of Greek prose. Journal of the Royal Statistical Society A 128, 169-233.
Morton, A.Q., Levison, M. (1966). Some indicators of authorship in Greek prose. In: Leed, J. (ed.), The Computer and Literary Style: 141-179. Kent, Ohio: Kent State UP.
Morton, A.Q. & McLeman, J. (1966). Paul, the man and the myth. London: Hodder and Stoughton.
Niehaus, B. (1994). Untersuchungen zur Satzlängenhäufigkeit im Deutschen. Göttingen: Staatsexamensarbeit.
Niehaus, B. (1997). Untersuchungen zur Satzlängenhäufigkeit im Deutschen. Glottometrika 16, 213-275.
Niehaus, B. (2001). Die Satzlängenverteilung in literarischen Prosatexten der Gegenwart. In: Uhlířova, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a linguistic paradigm: levels, constituents, constructs. Festschrift in honour of Ludek Hřebíček: 196-214. Trier: WVT.
Ommen, E. (2003). Quantitative Untersuchungen zur Syntax des Deutschen. Staatsexamensarbeit, Göttingen.
Parker, H.A. (1889). Curves of literary style. Science 13, 246.
Parolková, O. (1970). Determinace substantiva a délka vety. Filologické Studie 2, 29-39.
Rheinländer, N. (2000). Satzlängen in niederdeutschen und niederländischen Texten. Staatsexamensarbeit, Göttingen.
Rohrmann, Bernd (1974). Psychometrische und textstatistische Studien zu syntaktischen Variablen. Hamburg: Buske.
Rottmann, O. (2001). Sentence length in Old Church Slavonic. In: Uhlířová, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a Linguistic Paradigm: Levels, Constituents, Constructs. Festschrift in Honour of Ludek Hřebiček: 251-255.Trier: WVT.
Roukk, M. (2001). Satzlängen im Russischen. In: Best, K.H. (ed.), Häufigkeitsverteilungen in Texten: 211-218. Göttingen: Peust & Gutschmidt.
Roukk, M. (2001a). Satzlängen in Texten von Anton Tschechow. Göttinger Beiträge zur Sprachwissenschaft 5, 113-120.
Schindelin, C. (2005). Die quantitative Erforschung der chinesischen Sprache und schrift. In: Köhler, R., Altmann, G., Piotrowski, R.G. (2005), Quantitative Linguistics - An International Handbook: 947-970. Berlin: de Gruyter.
Sherman, L.A. (1888). Some observation upon the sentence-length in English prose. University of Nebraska Studies 1, 119-130.
Sichel, H.S. (1971). On a family of distributions particularly suited to represent long-tailed data. In: Laubscher, N.F. (ed.), Proceedings of the Third Symposium on Mathematical Statistics held on 18 and 19 May in the NRIMS: 51-97. Pretoria: CSIR Special Report WISK 89.
Sichel, H.S. (1974). On a distribution representing sentence-length in prose. J. of the Royal Statistical Society A 137, 25-34.
Sigurd, B., Eeg-Olofsson, M., & van de Weijer, J. (2004). Word length, sentence length and frequency - Zipf revisited. Studia Linguistica 58, 37-52.
Spang-Hanssen, H. (1963). Sentence-length and statistical linguistics. Structures and Quanta: 58-72. Copenhagen: Munksgaard.
Strehlow, M. (1997). Satzlängen in pädagogischen Fachartikeln des 19. Jahrhunderts. Göttingen: Staatsexamensarbeit.
Uhlířová, L. (2001). On word length, clause length and sentence length in Bulgarian In: Uhlířova, L., Wimmer, G., Altmann, G., Köhler, R. (Eds.), Text as a Linguistic Paradigm: Levels, Constituents, Constructs. Festschrift in Honour of Ludek Hřebiček: 266-282. Trier: WVT.
Vašak, P. (1974). Dlina slova i dlina predloženija v tekstach odnogo avtora. In: Voprosy statističeskoj stilistiki: 314-329. Kiev: Naukova dumka.
Vetulani, Z. (1989). Linguistic Problems in the Theory of Man-Machine Communication in Natural Language. Bochum: Brockmeyer.
Wake, W.C. (1957). Sentence-length distribution of Greek authors. J. of the Royal Statistical Society A 120, 331-346.
Williams, C.B. (1940). A note on the statistical analysis of sentence length as a criterion of literary style. Biometrika 31, 356-361.
Williams, C.B. (1970). Style and Vocabulary: Numerical Studies. London: Griffin.
Wimmer, G., Altmann, G. (1999). Thesaurus of univariate discrete probability distributions. Essen: Stamm.
Wittek, M. (1995). Zur Entwicklung der Satzkomplexität im gegenwärtigen Deutschen. Göttingen: Staatsexamensarbeit.
Wittek, M. (2001). Zur Entwicklung der Satzlänge im gegenwärtigen Deutschen. In: Best, K.-H. (ed.), Häufigkeitsverteilungen in Texten: 219-247. Göttingen: Peust & Gutschmidt
Yu, X. (2002). Quantitative Aspekte in pädagogischen Fachartikeln des 19. Jahrhunderts. Magisterarbeit, Göttingen.
Yule, G.U. (1939). On sentence-length as a statistical characteristic of style in prose: with application to two cases of disputed authorship. Biometrika 30, 363-390.
Yule, G.U. (1944). A Statistical Study of Literary Vocabulary. Cambridge: University Press.