Sound change

1. Problem and history

The approach is based on Zipf´s Principle of least effort according to which the increasing production effort of a sound increases the probability of its change (Zipf 1935, 1949). Boretzky (1977: 119) says it explicitely: “Die Sprecher sind bestrebt, die Laute beizubehalten, zu deren Artikulation wenig Anstrengung erforderlich ist, und die Laute als erste zu verändern oder ganz wegfallen zu lassen, deren Hervorbringung besonders viel Energie erfordert.“ The first quantification goes back to Job (1983) who derived a formula for the probability of change depending on articulation effort. Since articulation effort is merely one side of Zipf´s principle, the effort of the hearer in perceiving and decoding the sound must be taken into account, too. The first extended model was derived by Job and Altmann (1985) whose further extension was performed by Prün (1995).

2. Hypothesis

The probability of change of a sound is a function of its articulation and perception effort. (Job, Altmann 1985)

“Articulation effort” is the energy necessary to utter the sound. It can be measured e.g. by muscle participation in articulation. “Perception effort” could be measured as a function of the proportion of confusions of the given sound with other sounds (cf. Benzecri 1970; Clarke 1957; Conrad 1963; Conrad, Hull 1964; Gersic, Naumann, Altmann 1985; Klatt 1968; Miller, Nicely 1976; Nakatani 1972; Singh 1966, 1971; Thürmann 1974; Tversky 1977; Wickelgren 1965a,b,c, 1966a,b,c; Wilson 1963).

3. Derivation

3.1. The “effort” model

Let 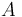$A$ be the articulation effort of the speaker, 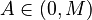$A\in(0,M)$, then the perception effort of the hearer is its complement, i.e. 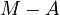$M - A$. Let further 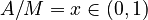$A/M = x \in (0,1)$ be the normed articulation effort and 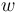$w$ the need for change. Then it holds for this need that

(1) $\frac{dw}{dx} = \frac{aw}{1-x} - \frac{bw}{x}$.

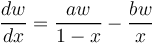One assumes that the greater 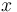$x$ (= normed effort), the greater the need for change with the speaker (= 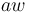$aw$) and the smaller with the hearer (= 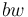$bw$). The solution of (1) yields

(2) $w = K(1-x)^{-a}x^{-b}, \quad 0<x<1$,

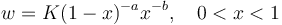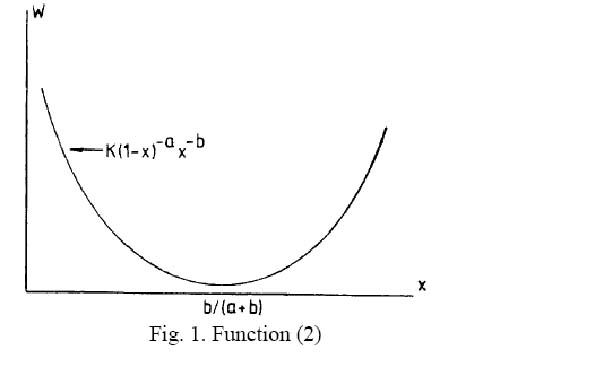
presented graphically in Fig. 1.

Fig. 1. Function (2)

If we consider 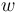$w$ as the probability of the need for change, then 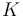$K$ is the norming constant which can be obtained as the usual beta function, i.e. we obtain finally the probability function

(3) $f_w(x) = \frac{1}{B(1-a, 1-b)}(1-x)^{-a}x^{-b}, \quad 0<x<1$.

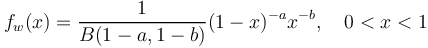The minimum of this curve is 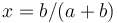$x = b/(a+b)$. In order to estimate the probability of change, we use the distribution function of (3) and compute the probability of a change of a sound as follows.

(a) If the effort of the speaker is 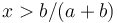$x > b/(a+b)$, then we compute

(4) $P_w(x) = \frac{1}{B(1-a, 1-b)}\int_{b/(a+b)}^{x}(1-x)^{-a}x^{-b}dx, \quad 0<x<1$,

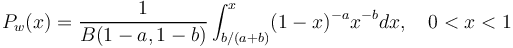i.e. the plane under the curve from its minimum to 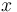$x$.

(b) If the effort of the speaker is 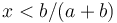$x < b/(a+b)$, then we compute

(5) $P_w(x) = \frac{1}{B(1-a, 1-b)}\int_x^{b/(a+b)}(1-x)^{-a}x^{-b}dx, \quad 0<x<1$.

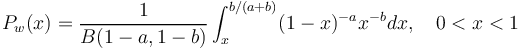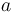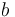No testing has been performed as of yet and the parameters $a$ and $b$ have not been interpreted physically.

3.2. Prün´s extension

Since in the sense of Zipf a change depends also on the frequency of the sound, Prün (1995) extended the above formula inserting in it the relative frequency 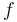$f$ of the sound and obtained

(6) $y = K(1-x)^{-af}\cdot x^{-b(1-f)}$.

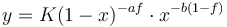The differential equation leading to this result is

(7) $\left( \frac{dy}{dx} + \frac{dy}{df}\right)\frac{1}{y} = af - b (1-f)+b \ln x - a \ln (1-x)$,

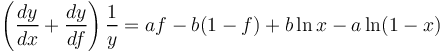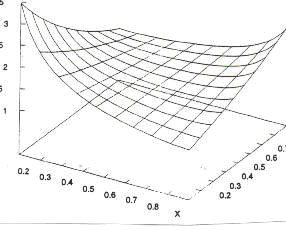
but it has not been interpreted yet. A graphical example can be seen in Fig. 2.

Fig. 2. Function (6) with special values (Prün 1995)

4. Authors: U. Strauss, G. Altmann

5. References

Job, U. (1983). Bemerkungen zu einer theoreti¬schen Konzeption von Sprachwandel. In: K.-H. Best und J. Kohlhase (eds.), Exakte Sprachwandelforschung: 5 – 19. Göttingen: Edition Herodot.

Job, U., Altmann, G. (1985). Ein Modell der anstrengungsbedingten Lautveränderung. Folia Linguistica Historica 6, 401-407.

Lehfeldt, W. (2005). The fall of jers in the light of Menzerath´s law. In Grzybek, P. (ed.), Word length studies and related issues: 215-218. Boston/Dordrecht: Kluwer.

Lehfeldt, W., Altmann, G. (2000). Padenie reducirovannych v svete zakona P. Mencerata. Russian Linguistics 26, 327-344.

Lehfeldt, W., Altmann, G. (2003). The process of the fall of the reduced vowels in Old Russian in the light of the Piotrovskii law. Russian Lingusitics 27, 141-149.

Prün, C. (1995). Die linguistischen Hypothesen von G.K. Zipf aus systemtheoretischer Sicht. Trier: Magisterarbeit.