User:Ahans

Word length and frequency

1. Problem and history

There are two problems that must be strictly separated:

(a) The use of words of specific length in texts. Here word forms are meant and neither the size of the lexicon nor the number of phonemes in the phoneme inventory are relevant. Other properties like polysemy, polytexty, or synthetism can be added for modelling textual word length.

(b) Frequency as a factor of lemma construction in the dictionary, where frequency is taken from a frequency dictionary, and the dictionary size, as well as the size of the phoneme inventory, are relevant.

In (b), problems arise because the size of the dictionary can be merely coarsely estimated. There are even authors considering it infinite (cf. Piotrowski, Bektaev, Piotrovskaja 1985; Kornai 2002), which is a reasonable assumption. If, however, it is considered as a fixed finite value, it can be taken into account. Further, frequency dictionaries strongly depend on the kind of the analyzed texts. In order to secure a reliable frequency dictionary even for a short time period, an astronomical number of words must be counted.

Problem (a) is easily solvable but it must be considered for individual texts or group of texts from the same author. Here we consider merely the problem of dependence of word form length on its frequency in texts. In case of rejecting this relationship in some texts, further variables can be joined, e.g. number of meanings.

Another problem is frequency of occurrence and duration (→). G.K. Zipf (1935:25) set up two hypotheses on the relation of frequency and length:

(I) “The magnitude of words tends, on the whole, to stand in an inverse (not necessarily proportionate) relationship to the number of occurrences.” His second hypothesis on the variety of words occurring x-times is simply that of the distribution of word frequency (→).

Zipf himself demonstrated the inverse of (I) using Kaeding´s frequency dictionary of German (Kaeding 1897), i.e. he simply demonstrated the distribution of lengths which turned out to be monotone decreasing (→ word length). Baker (1951) used the letters of a woman with psychic deseases and divided the words in frequency groups; some authors use frequency directly, other ones use the ranks as independent variable. Word length has been counted in terms of the number of phonemes (e.g. Miller, Newman, Friedman 1958) or syllables. Different empirical formulas have been proposed (Belonogov 1962, Guiraud 1954, Kalinin 1964, Guiter 1977). Köhler (1986) discovered an oscillation of lengths and Köhler, Zörnig, Brinkmöller (1990) smoothed the data by taking gliding means. Grzybek, Altmann (2002) and Strauss, Grzybek and Altmann (2005) have shown the dependence of length on frequency in ten languages using individual texts, but other researchers rather use corpora representing mixed samples. Different aspects of this relationship have been shown in Strauss, Grzybek, Altmann (2005). Krott (1996, 2002) stated the same relationship between frequency and morpheme length.

2. Hypothesis

The mean syllabic length (y) of word forms in texts decreases with their frequency of occurrence (x).

Here each form is considered separately and the mean length of all forms with the same frequency is considered y. Since frequency can be considered in relative form, x can be considered continuous. Further hypotheses can be derived from the above-mentioned one, e.g. shorter forms of the word are more frequent than its longer forms (e.g. case, modus, aspect, tenses). Or, derivates and compounds of a lexeme occur more seldom than the lexeme itself.

3. Derivation

Köhler (1986), Strauss, Grzybek, Altmann (2005) start from the assumption that the relative rate of change of mean word length decreases proportionally to the relative rate of change of the frequency, as is very usual in synergetic linguistics. If zero-syllabic clitics are considered parts of the following words, then the mean length cannot take values less than 1. Thus the differential equation is

(1) $\frac{dL}{L-1}= -b\frac{dF}{F}$

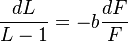
from which the well-known formula

(2) $L=aF^b+1,\quad a>0,\quad b<0$

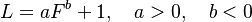
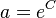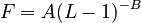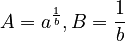follows. Here $a = e^C$ (C being the integration sonstant). If one considers frequency as depending on length, inversion yields $F = A(L-1)^{-B}$ with $A =a^\frac{1}{b},B =\frac{1}{b}$. (2) is a special case of of the unified derivation (see Introduction, 4.1). Other empirical formulas can be found in the references.

Example. Russian text

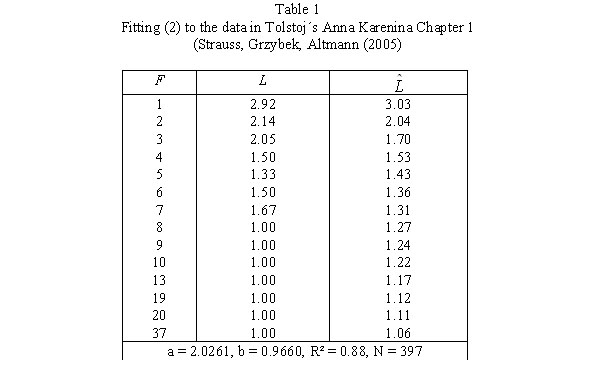
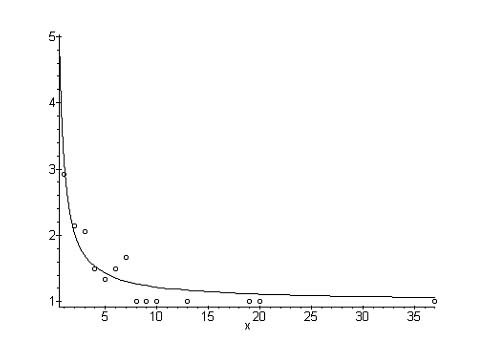
Strauss, Grzybek, Altmann (2005) present the result for the first chapter of Tolstoj´s Anna Karenina. For each frequency class the mean word-form length has been computed. Zero-syllabic prepositions (k, s, v) were considered proclitics. Frequency classes containing fewer than 10 records were pooled and the unweighted average was computed. The result is presented in Table 1 and Fig. 1. In the frist column, the frequency classes are shown, in the second the observed mean word form lengths, and in the third the theoretical mean lengths according to (2).

Table 1

Fitting (2) to the data in Tolstoj´s Anna Karenina Chapter 1

(Strauss, Grzybek, Altmann (2005)

Fig. 1. Fitting (2) to the data from Anna Karenina Ch. 1.

4. Authors: U. Strauss, G. Altmann

5. References

Baker, S.J. (1951). A linguistic law of constancy: II. The J. of General Psychology 44, 113-120. Belonogov, G.G. (1962). O nekotorych statističeskich zakonomernostjach ruskoj pis´mennoj reči. Voprosy jazykoznanija 11/1, 100-101.

Breiter, M.A. (1994). Length of Chinese words in relation to their other systemic features. J. of Quantitative Linguistics 1, 224-231.

Bürmann, C., Frank, H., Lorenz, L. (1963). Informationstheoretische Untersuchungen über Rang und Länge deutscher Wörter. Grundlagenstudien aus Kybernetik und Geisteswissenschaft 4 (3-4), 73-90.

Fenk-Oczlon, G. (2001). Familiarity, information flow, and linguistic form. In: Bybee, J., Hopper, P. (eds.). Frequency and the emergence of linguistic structure: 431-448. Amsterdam: Benjamins.

Gieseking, K. (2002). Untersuchungen zur Synergetik der englischen Lexik. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 387-433. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/

Grzybek, P., Altmann, G. (2002). Oscillation in the frequency-length relationship. Glottometrics 5, 97-107.

Guiraud, P. (1954). Les caractères statistiques du vocabulaire. Essai de méthodologie. Paris: P.U.F.

Guiter, H. (1977). Les relations /frequence-longeuer-sens/ des mots (langue romanes et anglais). XVI Congresso Internazionale di Linguistica e Filologia Romanza, Napoli, 15-20 Aprile 1974, 373-381. Napoli: Macchiaroli.

Hammerl, R. (1990). Länge - Frequenz, Länge - Rangnummer. Überprüfung von zwei lexikalischen Modellen. Glottometrika 12, 1-24.

Hammerl, R. (1991). Untersuchungen zur Struktur der Lexik: Aufbau eines lexikalischen Basismodells. Trier, WVT.

Herdan, G. (1966). The advanced theory of language as choice and chance. Berlin, Springer.

Kaeding, F.W. (1897-98). Häufigkeitswörterbuch der deutschen Sprache. Steglitz: Selbstverlag.

Kalinin, V.M. (1964a). O statistike literaturnogo teksta. Voprosy jazykoznanija Nr. 1, 123-127.

Köhler, R. (1986). Zur linguistischen Synergetik: Struktur und Dynamik der Lexik. Bochum: Brockmeyer.

Köhler, R., Zörnig, P., Brinkmöller. (1990). Differential equation models for the oscillation of the word length as a function of the frequency. Glottometrika 12, 25-40.

Kornai, A. (2002). How many words are there? Glottometrics 4, 61-86.

Krott, A. (1996). Some remarks on the relation between word length and morpheme length. J. of Quantitative Linguistics 3, 29-37.

Krott, A. (2002). Ein funktionalanalytisches Modell der Wortbildung. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 75-126. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/

Leopold, E. (1997). Frequency spectra within word length classes. In: Third International Conference on Quantitative Linguistics, August 26-29, 1997, Helsinki, Finland: 156. Helsinki: Monila.

Leopold, E. (1998). Stochastische Modellierung lexikalischer Evolutionsprozesse. Hamburg: Kovač

Leopold, E. (2000a). Length-distribution of words with coinciding frequency. In: Proceedings of the fourth conference of the International Quantitative Linguistic Association, Prague, August 24-26: 76-77.

Miller, G.A., Newman, E.B., Friedman, E.A. (1958). Length-frequency statistics for written English.. Information and Control 1, 370-389.

Miyajima, T. (1992). Relationship in the length, age and frequency of Classical Japanese words. Glottometrika 13, 219-229.

Piotrowski, R.G., Bektaev, K.B., Piotrovskaja, A.A. (1985). Mathematische Linguistik. Bochum, Brockmeyer.

Sanada, H. (1999). Analysis of Japanese vocabulary by the theory of synergetic linguistics. J. of Quantitative Linguistics 6, 239-251.

Strauss, U., Grzybek, P., Altmann, G. (2005). Word length and word frequency. In: Grzybek, P. (ed.), Word length studies and related issues: 255-272. Boston/Dordrecht: Kluwer.

Tuldava, J. (1995). Methods in quantitative linguistics. Trier: WVT.

Zipf, G.K. (1932). Selected studies of the principle of relative frequency in language. Cam-bridge, Mass.: Harvard University Press.

Zipf, G.K. (1935).The psycho-biology of language. Boston: Houghton Mifflin.