Difference between revisions of "Definition chains"
| Line 75: | Line 75: | ||
| + | <div align="center">[[Image:Figur2_Def.jpg]]</div> | ||
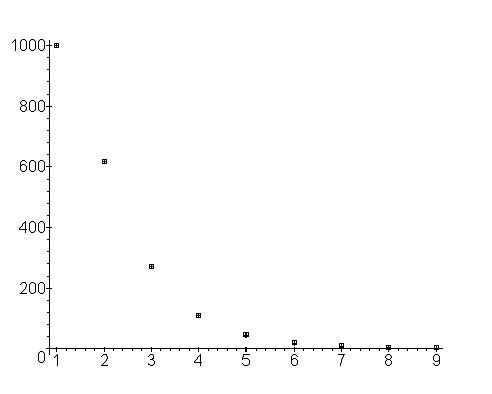
<div align="center">Fig. 1. Fitting (2) to Polish nouns (with repetition)</div> | <div align="center">Fig. 1. Fitting (2) to Polish nouns (with repetition)</div> | ||
| − | |||
<div align="center">[[Image:Figur3_Def.jpg]]</div> | <div align="center">[[Image:Figur3_Def.jpg]]</div> | ||
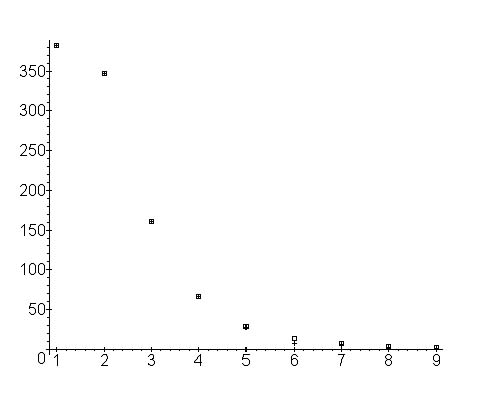
<div align="center">Fig. 2. Fitting (2) to Polish data (without repetition)</div> | <div align="center">Fig. 2. Fitting (2) to Polish data (without repetition)</div> | ||
| − | |||
'''3.2. Hammerl´s version B (1989a''') | '''3.2. Hammerl´s version B (1989a''') | ||
Revision as of 07:59, 18 May 2006
1. Problem and history
Take a noun from a monolingual dictionary and seek in its definitions (explications) the noun which is its genus proximum, i.e. only the relation of inclusion is relevant. For example cat is an animal; then look at animal to find that it is a living creature, which in turn is an organism, etc. In this way one obtains a definition chain. Thus a definition chain is a sequence of nouns in which the ith noun is member of the class encompassed by the (i+1)st noun, or in other words, the (i+1)st noun is the genus proximum of the ith noun. There are, of course, sometimes two or more genera proxima giving rise to lexeme nets. Definition chains have different length. Taking a sample from a dictionary one sees that the number of different nouns on each higher level is smaller than that on lower levels. The first empirical observations on chains have been made by R. Martin (1974), the first model which held only for Martin´s data was presented by Altmann and Kind (1983), who called this phenomenon Martin´s law. Hammerl´s model (1987a) presented below is widely applicable, however there are many alternative ways of establishing definition chains (cf. Sambor, Hammerl 1991, Schierholz 1989) and their final forms depends not only on criteria but also on the size of the dictionary. If one considers all meanings of a noun, one obtains lexeme nets which can be treated as graphs, having different properties. Up to now no laws have been found for the construction of lexeme nets.
2. Hypothesis
The number of nouns in a set of definition chains is the smaller the higher the abstraction (generality) level of the nouns.
“Abstraction level” or “generality” is the position of a noun in the chain, e.g. in cat – animal – creature – organism – system the first noun cat has position (level, degree) 1, animal has degree 2, creature 3 etc. (cf. Kisro-Völker 1984).
The hypothesis involves that the resulting distribution is monotone decreasing.
Critical points: (1) The lowest level can begin with 0 or 1, it is merely a convention. We use here 1.
(2) As 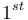 -level nouns either all nouns are admitted or only those which are not genera proxima of another nouns.
-level nouns either all nouns are admitted or only those which are not genera proxima of another nouns.
(3) There are three kinds of counting the number of nouns on a given level: (i) one counts all lexemes, (ii) one counts only different lexemes, (iii) one counts a given lexeme only on its highest level. It depends on the problem examined. (4) In some languages compound nouns can strongly prolong the chains. One can take them into account or not.
(5) The choice of the sampling dictionary is of great improtance. Great dictionaries prolong the chains.
(6) The existence of different genera proxima for a noun leads to the problem of lexeme nets but it can be solved in that one takes only one of them.
(7) In circular definitions the last noun should be eliminated, e.g. Stall – Gebäude – Bauwerk – Gebäude.
(8) Since dictionaries do not care for unambiguity of chains, one can apply one owns competence in completing or changing them. Such a procedure strongly depends on the erudition of the researcher.
(9) Not nominal lexemes should be left out, e.g. something that.
(10) In German every verb can be converted to noun (arbeiten - das Arbeiten). In these cases the converted noun can be replaced by the equivalent noun (Arbeit).
(11) It is not known whether the above laws hold also for other word classes or other relations between lexemes.
3. Derivation
3.1. Hammerl´s version A (1987a)
Assumptions:
(i) The number of lexemes on level x+1 is proportional to the power of that on level x, i.e. 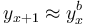 .
.
(ii) The number of lexemes on level x+1 is inversely proportional to the power of the level itself, i.e 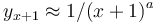 .
.
Putting these assumptions together one obtains
(1)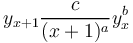 .
.
where c is the proportionality constant. In practice, formula (1) is used since the solution
(2) 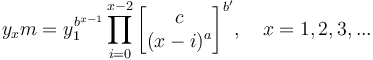 .
.
is neither illuminating nor practical. If one considers it a probability distribution, it must be normed. The estimation of the parameters a,b,c can be performed using the first four observed values. Let
(3)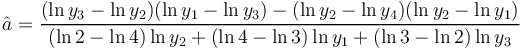
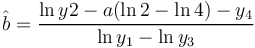
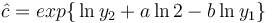
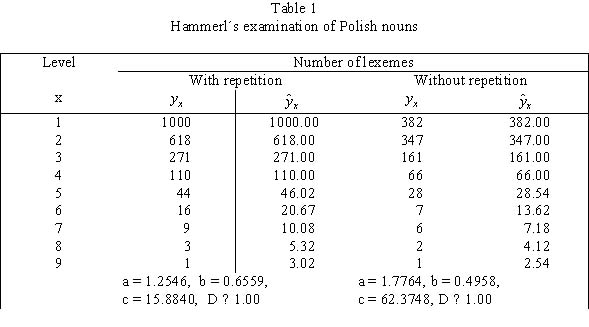
Example: Definition chains for Polish nouns
Hammerl (1987b) constructed definition chains for 1000 Polish nouns using two methods: (a) A lexeme can be repeated, i.e. the same lexeme can occur on different levels but it is counted only once on each particular level. (b) Lexemes cannot be repeated, i.e. if a lexeme occurs on different levels (in different chains), it is counted only on its highest level. The results are shown in Table 1.
The fitting is so good that the empirical and the theoretical points in the graphs cannot be distinguished.
3.2. Hammerl´s version B (1989a)
In Hammerl´s version A the lexemes were numbered beginning from the most concrete level upwards, i.e. (DC = definition chain)
In version B the most general noun of every chain is assigned level 1, the next one level 2 , etc., i.e. the chains begin “from above”
Hammerl starts from the assumption that for the speaker a very general way of expressing himself is sufficient, thus he has the tendency to shorten the chains which is in agreement with his least effort; the hearer, on the contrary, requires very concrete designations, in order to reduce his own decoding effort. Thus definition chains develop in language dynamically. Consider a a constant depending on dictionary size, -bx the negative influence of the speaker upon the given level and cx the effort of the hearer to brake the intention of the speaker, one obtains the classical steady state situation of the diversification process (à) (with displacement) given as
(5)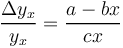
whose solution after reparametrisation [(c-b)/c = q, a/(a-b) = k-1 and yx = Px] yields the 1-displaced negative binomial distribution
(6)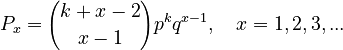
If one counts a noun on each level only once, the distribution need not be monotone decreasing.
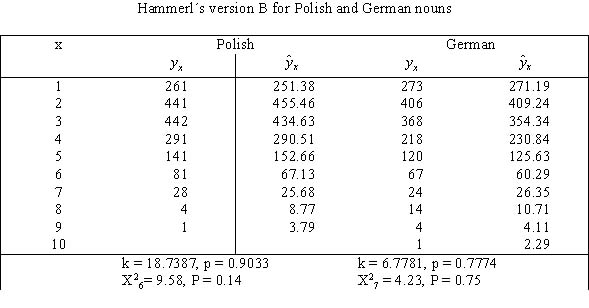
Example: Definition chains for Polish and German nouns
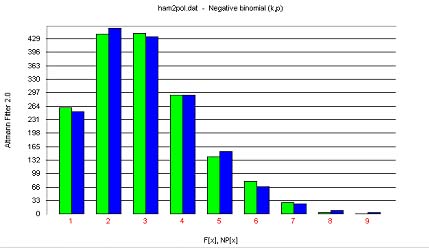
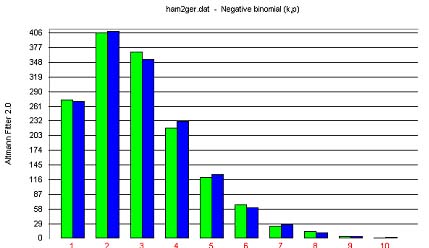
Hammerl (1989a: 134) showed the distribution of Polish and German nouns in definition chains built according to his version B as given in Table 2.
The results of fitting are very good in both cases.
3.3. Hammerl´s law
Another aspect of definition chains is the number (frequency) of lexemes occurring x-times in all examined chains. Here the ordering on different levels is irrelevant, the point is the frequency of occurrence. Hammerl (1991b) excludes two extreme possibilities: (a) All lowest level nouns have their own individual chains, not intersecting with other ones, i.e. no lexeme of higher level is common to two chains. (b) The nouns are semantically in such a close relationship that they all have one common “ancestor”. Since the selection of nouns from the dictionary must be random, these cases are for a sample very improbable. For the whole dictionary they are impossible. Hammerl (1991b) used a continuos approach leading to Menzerath´s law (zeta distribution). Unfortunately, the fitting could be made satisfactory only if one modified the distribution a posteriori. In discrete terms Hammerl´s approach can be presented in the form
(7)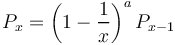
which means that the probability of lexemes occurring in all examined chains x-times is proportional to those occurring x-1 times, the proportionality function being g(x) = (1-1/x)a. Here we assume the same mechanism but define the proportionality as
(8) 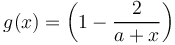
i.e.
(9)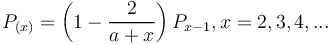
resulting in the Johnson-Kotz distribution (called sometimes Yule-Simon d.)
(10)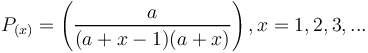
which is a special case of the unified theory (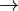 ) formula (10) substituting
) formula (10) substituting 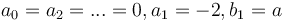 .
.
Example: German definition chains
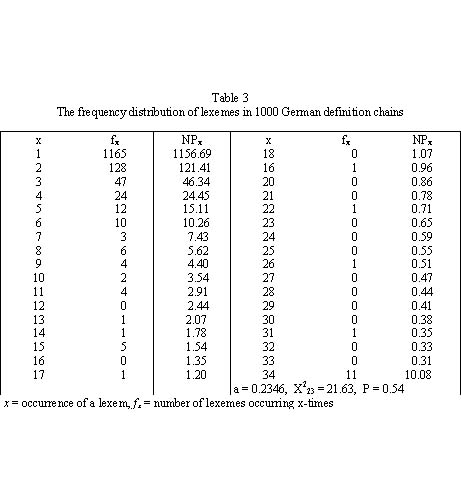
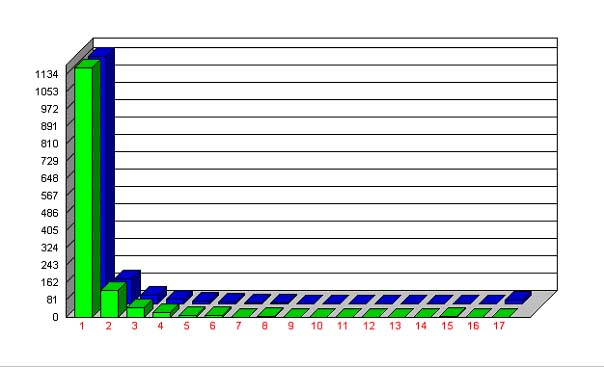
Hammerl (1991b) and Hammerl, Sambor (1997) showed data from 1000 German definition chains as given in Table 3. The frequencies greater than or equal to x = 34 were pooled in the last class. The results of fitting (10) are in the third column of Table 3 (Fig. 5). The classes were pooled so that each theoretical frequency was greater than 1.
The result of fitting is very good.
4. Authors: U. Strauss, G. Altmann
5. References:
Altmann, G. (1991b). Definitionsfolgen und Lexemnetze. In: Sambor, J., Hammerl, R. (eds.) 1991: 188-198.
Altmann, G., Bagheri, D., Goebl, H., Köhler, R., Prün, C. (2002). Einführung in die quantitative Lexikologie. Götingen: Peust & Gutschmidt.
Altmann, G., Kind, B. (1983). Ein semantisches Gesetz. Glottometrika 5, 1-13.
Bagheri, D. (1996). Review of Hammerl, R., Sambor, J. (eds.) 1991. Journal of Quantitative Linguistics 3, 152-168.
Bagheri, D. (2002). Definitionsfolgen und Lexemnetze. In: Altmann, G., Bagheri, D., Goebl, H., Köhler, R., Prün, C., Einführung in die quantitative Lexikologie: 94-133. Göttingen: Peust & Gutschmidt.
Gołębiewska, E. (1989). Gniazda pojęcziowe v Małym Slowniku Jzyka Polskiego. Warszawa: Diss.
Gołębiewska, E. (1991). Statistische Strutkur der Lexemnetze in der polnischen und deutschen Sprache – eine vergleichende Analyse. In: Sambor, J., Hammerl, R. (eds.) 1991: 120-128.
Hammerl, R. (1987). Prawa językowe we współczesnej kwantytatywnej lingwistyce modelowej (na przykladie tzw. Prawa Martina). Poradnik Językowy 6, 414-428.
Hammerl, R. (1987a). Untersuchungen zur mathematischen Beschreibung des Martingesetzes der Abstraktionsebenen. Glottometrika 8, 113-129.
Hammerl, R. (1987b). Untersuchungen zur mathematischen Beschreibung des Martingesetzes der Abstraktionsebenen. Glottometrika 9, 105-120.
Hammerl, R. (1988). Neue theoretische Untersuchungen im Zusammenhang mit dem Martingesetz der Abstraktionsebenen. Glottometrika 9, 105-120.
Hammerl, R. (1989a). Neue Perspektiven der sprachlichen Synergetik: Begriffsstrukturen – kognitive Gesetze. Glottometrika 10, 129-140.
Hammerl, R. (1989b). Untersuchung struktureller Eigenschaften von Begriffsnetzen. Glottometrika 10, 141-154.
Hammerl, R. (1990a). A contribution to the examination of semantic relations between lexemes. In: Bock, H.H., Ihm, P. (eds.), Classification, data analysis, and knowledge organization. Models and methods of applications: 149-155. Berlin-Heidelberg: Springer.
Hammerl, R. (1990e). Gniazda pojęcowie. Przegląd problemów. Poradnik Językowy 9-10, 680-693.
Hammerl, R. (1991a). Definition von Grundbegriffen für die Untersuchung von Definitionsfolgen und Lexemnetzen. In: Sambor, J., Hammerl, R. (eds.) 1991: 2-12.
Hammerl, R. (1991b). Messung der Stärke von semantischen Relationen zwischen Lexemen. In: Sambor, J., Hammerl, R. (eds.) 1991: 75-96.
Hammerl, R. (1991c). Methodologische und methodische Probleme der Erstellung von Definitionsfolgen und Lexemnetzen. In: Sambor, J., Hammerl, R. (eds.) 1991: 13-37.
Hammerl, R. (1991d). Überprüfung des Martingesetzes I an deutschem Sprachmaterial. In: Sambor, J., Hammerl, R. (eds.) 1991: 50-64.
Hammerl, R. (1991e). Untersuchungen von Definitionsfolgen und Lexemnetzen: eine einführende Bibliographie. In: Sambor, J., Hammerl, R. (eds.) 1991: 200-204.
Hammerl, R. (1991f). Zur Untersuchung der semantischen Struktur der Lexik. Vergleich zweier Modelle. In: Sambor, J., Hammerl, R. (eds.) 1991: 174-186.
Hammerl, R., Rogalińska, A. (1991). Erstellung und Analyse von Lexemnetzen mit dem PC-Programm NETZE. In: Sambor, J., Hammerl, R. (eds.) 1991: 157-173.
Hammerl, R., Sambor, J. (1993a). O statystycznych prawach jezykowych. Warszawa: Polskie Towarzystwo Semiotyczne.
Hammerl, R., Sambor, J. (1997). Miary stopnia bliskości semantycznej leksemów. In: J.Sambor (ed.), Z zagadnień kwantytatywnej semantyki kogntiywnej: 217-238. Warszawa: Polskie Towarzystwo Semiotyczne.
Hammerl, R., Schulz, K.P. (1988). Untersuchungen von Strukturen sprachlicher Begriffe am Beispiel von Abstraktionsstrukturen. Referat auf der Jahrestagung der Gesellschaft für Klassifikation. Darmstadt
Jankiewicz, M. (1991). Vergleichende Analyse von Definitionsfolgen aus zwei polnischen Wörterbüchern. In: Sambor, J., Hammerl, R. (eds.) 1991: 39-49.
Januszkiewicz, N.A. (1997). Angielskie gniazda leksykalne. Wybrane aspekty analizy semantycznej pojęć końcowych. In: J.Sambor (ed.), Z zagadnień kwantytatywnej semantyki kogntiywnej: 175-213. Warszawa: Polskie Towarzystwo Semiotyczne.
Kisro-Völker, S. (1984). On the measurement of abstractness in lexicon. Glottometrika 6, 138-151.
Komuda, J. (1986). Budowa ciągów definicyjnych na podstawie 6-tomowego „Rečnika srpskohrvatskogo književnogo jezyka. Warszawa: Diss.
Lewczuk, J. (1991). Homonyme und polyseme Lexeme in Lexemnetzen. In: Sambor, J., Hammerl, R. (eds.) 1991: 129-152.
Martin, R. (1974). Syntaxe de la définition lexicographique: étude quantitative des définissants dans le « Dictionnaire fondamental de la langue francaise. In David, J., Martin, R. (eds.), Statistique et linguistique: 61-71. Paris: Klincksieck.
Sambor, J. (1983). O budowie tzw. ciągów definicyjnych (na material definicji leksykalnych) Biuletyn PTJ 40, 151-165.
Sambor, J. (1991). Definitionsfolgen und Suche nach semantischen Indefinibilien. In: Sambor, J., Hammerl, R. (eds.) 1991: 65-73.
Sambor, J. (1997a). Ciągi definicyjne i gniazda leksykalne jako nowy temat semantyki leksykalnej. In: J.Sambor (ed.), Z zagadnień kwantytatywnej semantyki kogniywnej: 9-23. Warszawa: Polskie Towarrzystwo Semiotyczne.
Sambor, J., Hammerl, R. (1997). Gniazda leksykalnne i pojęciowe w słowniku języka niemiec-kiego (na materilae słownika Handwörterbuch der deutschen Gegenwartssprache). In: J.Sambor (ed.), Z zagadnień kwantytatywnej semantyki kognitywnej: 147-173. Warszawa: Polskie Towarzystwo Semiotyczne.
Schierholz, St. (1989). Kritische Aspekte zum Martinschen Gesetz. Glottometrika 10, 108-128.
Schulz-Otto, K.-P., Hammerl, R. (1988). Untersuchungen sprachlicher Begriffe – am Beispiel von Abtsraktheitsstrukturen. In. Wille, R. (ed.), Klassifikation und Ordnung. Studien zur Klassifikation 19, 221-224. Frankfurt: Indeks Verlag.
Szczekocka-Augustyn, A. (1997). Ciagi definicyjne w swiadomosci osób mówiacych (na materiale naczyn i mebli. In: Sambor, J. (ed.), Z zagadnień kwantytatywnej semantyki kogniywnej:69-105. Warszawa: Polskie Towarrzystwo Semiotyczne.
Wereszczyńska, B. (1997). Ciągi definicyjne w świadomości osób mówiących (na materiale nazw zwierząt). In: J.Sambor (ed.), Z zagadnień kwantytatywnej semantyki kogniywnej: 47-67. Warszawa: Polskie Towarrzystwo Semiotyczne.
Zagrodska, T. (1997). Ciągi definicyjne w świadomości osób mówiących (na materiale nazw roślin. In: J. Sambor (ed.), Z zagadnień kwantytatywnej semantyki kognitywnej: 33-46. War-szawa: Polskie Towarzystwo Semiotyczne.