Difference between revisions of "Syllable structure"
| (5 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
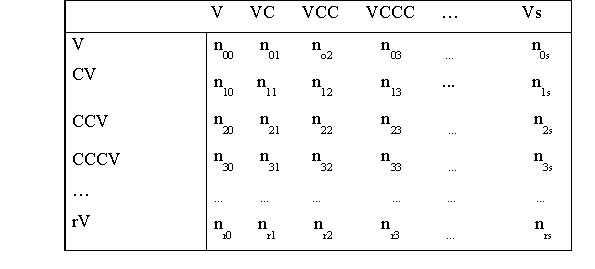
If syllables are coded in the canonical form, V, CV, CVC, etc. where the vowel (V) is the syllable nucleus and the consonant (C) is the periphery, we obtain a set of structural types whose number follows a specific two-dimensional distribution. The types can be presented in tabular form | If syllables are coded in the canonical form, V, CV, CVC, etc. where the vowel (V) is the syllable nucleus and the consonant (C) is the periphery, we obtain a set of structural types whose number follows a specific two-dimensional distribution. The types can be presented in tabular form | ||
| − | + | <div align="center">[[Image:Tabelle1_SS.jpg]]</div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Where the frequency of the type CVVCC is given as n12, i symbolizing the number of consonants before and j that behind the nucleus. There are at most r onsets and s codas in the syllable. Let <math>P_{ij}*</math> be the corresponding probability. | Where the frequency of the type CVVCC is given as n12, i symbolizing the number of consonants before and j that behind the nucleus. There are at most r onsets and s codas in the syllable. Let <math>P_{ij}*</math> be the corresponding probability. | ||
| Line 26: | Line 15: | ||
Starting from the unified theory we assume that the probabilities of syllable types are joined with the following proportionality relation | Starting from the unified theory we assume that the probabilities of syllable types are joined with the following proportionality relation | ||
| − | (1)<math> P_{i,j}* | + | (1)<math> P_{i,j}* \propto P_{i, j-1}*</math> |
| − | <math> P_{i,j}* | + | |
| + | <math> P_{i,j}* \propto P_{i-1, j}*</math> | ||
i.e. a class is proportional to its left or upper neighbour. In the first step Zörnig and Altmann (1993) used the simple Menzerathian relatioship (see Hierarchic relations) as proprotionality function and obtained | i.e. a class is proportional to its left or upper neighbour. In the first step Zörnig and Altmann (1993) used the simple Menzerathian relatioship (see Hierarchic relations) as proprotionality function and obtained | ||
| Line 40: | Line 30: | ||
where the norming constant is <math> P_{0,0}^{-1} = \sum_{i=0}^r \sum_{j=0}^s\frac{a^i b^j}{(i!)^k(j!)^m}</math> . | where the norming constant is <math> P_{0,0}^{-1} = \sum_{i=0}^r \sum_{j=0}^s\frac{a^i b^j}{(i!)^k(j!)^m}</math> . | ||
| − | Since the particular case examined (Indonesian) has a strong preference for the CVC type ( = <math>n_11</math>) the distribution must be modified and renormed. Weighting <math>P_11*</math> by β the other probabilities must be weighted so that <math> | + | Since the particular case examined (Indonesian) has a strong preference for the CVC type ( = <math>n_11</math>) the distribution must be modified and renormed. Weighting <math>P_11*</math> by β the other probabilities must be weighted so that <math>\beta P_11* + \alpha(1-P_11*) = 1</math>. As a result we obtain |
(4)<math> P_{i,j}= \begin{cases} \beta P_{i,j}*, & i=j=1 \\ \alpha P_{i,j}*, & i= 0,1,...,r,\quad j=0,1,...,s,\quad i \ne 1 or j \ne 1\end{cases}</math> | (4)<math> P_{i,j}= \begin{cases} \beta P_{i,j}*, & i=j=1 \\ \alpha P_{i,j}*, & i= 0,1,...,r,\quad j=0,1,...,s,\quad i \ne 1 or j \ne 1\end{cases}</math> | ||
| Line 63: | Line 53: | ||
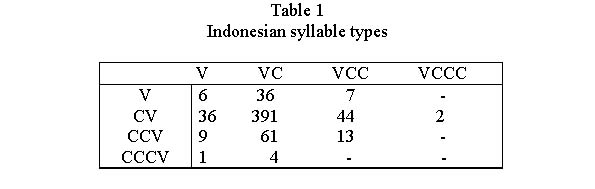
In about 15000 Indonesian word forms from different texts Zörnig and Altmann (1993) found 610 syllable types shown in Table 1. | In about 15000 Indonesian word forms from different texts Zörnig and Altmann (1993) found 610 syllable types shown in Table 1. | ||
| − | + | <div align="center">[[Image:Tabelle11_SS.jpg]]</div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Using (3), (4) and (5) they obtained | Using (3), (4) and (5) they obtained | ||
| + | <math>P_{i,j}= \begin{cases} 0.713P*_{i,j}, & i\ne 1 or j\ne 1 \\ 1.291P*_{i,j}, & i=j=1 \end{cases}</math> | ||
with | with | ||
| − | |||
| − | + | <math> P*_{i,j}=\frac{(o.014)6^{i+j}}{(i!)^{4.585}(j!)^{4.948}}, \quad 0\le i, j<4</math>. | |
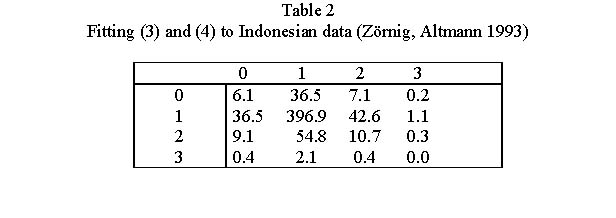
| − | + | The estimated parameters are: a = b = 6, k = 4.585, m = 4.948, α = 0.713, β = 1.291, <math>P*_{00}</math> = 0.014, N = 610 and the fitting is presented in Table 2. For example <math>NP_{12}</math> is computed as | |
| − | + | <math> NP_{1,2}= 610\frac{0.713(0.014)6^{1+2}}{1!^{4.585} 2!^{4.948}}=610(0.06985) = 42.61</math> . | |
| − | |||
| − | + | <div align="center">[[Image:Tabelle22_SS.jpg]]</div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The result is acceptable without testing. | The result is acceptable without testing. | ||
| − | 4. Authors: U. Strauss, G. Altmann | + | '''4. Authors''': U. Strauss, G. Altmann |
| + | |||
| + | '''5. References''' | ||
| + | |||
| + | '''Lee, Sank-Oak''' (1986). An explanation of syllable structure change. ''Korean Language Research 22, 195-213.'' | ||
| − | + | '''Vennemann, T.''' (1982) (ed.). Zur Silbenstruktur der deutschen Standardsprache. ''Silben, Segmente, Akzente: 261-305''. Tübingen: Narr. | |
| − | + | '''Zörnig, P., Altmann, G'''. (1993). A model for the distribution of syllable types. ''Glottometrika 14, 190-196''. | |
| − | |||
| − | Zörnig, P., Altmann, G. (1993). A model for the distribution of syllable types. Glottometrika 14, 190-196. | ||
Latest revision as of 12:54, 24 July 2006
1. Problem and history
If syllables are coded in the canonical form, V, CV, CVC, etc. where the vowel (V) is the syllable nucleus and the consonant (C) is the periphery, we obtain a set of structural types whose number follows a specific two-dimensional distribution. The types can be presented in tabular form
Where the frequency of the type CVVCC is given as n12, i symbolizing the number of consonants before and j that behind the nucleus. There are at most r onsets and s codas in the syllable. Let 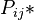 be the corresponding probability.
be the corresponding probability.
2. Hypothesis
The distribution of canonical syllable types abides by the (modified) bivariate Conway-Maxwell-Poisson distribution.
3. Derivation
Starting from the unified theory we assume that the probabilities of syllable types are joined with the following proportionality relation
(1)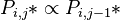
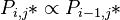
i.e. a class is proportional to its left or upper neighbour. In the first step Zörnig and Altmann (1993) used the simple Menzerathian relatioship (see Hierarchic relations) as proprotionality function and obtained
(2)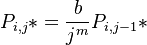
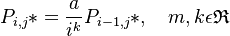
The solution of (2) yields
(3)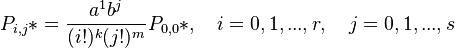
where the norming constant is 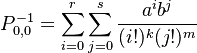 .
.
Since the particular case examined (Indonesian) has a strong preference for the CVC type ( = 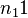 ) the distribution must be modified and renormed. Weighting
) the distribution must be modified and renormed. Weighting 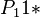 by β the other probabilities must be weighted so that
by β the other probabilities must be weighted so that 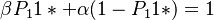 . As a result we obtain
. As a result we obtain
(4)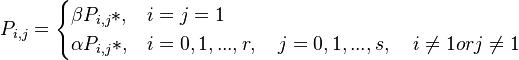
Zörnig and Altmann (1993) show also the estimators won from frequency classes as
(5)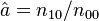
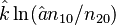
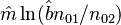
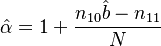
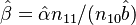
Example. Structure of Indonesian syllables
In about 15000 Indonesian word forms from different texts Zörnig and Altmann (1993) found 610 syllable types shown in Table 1.
Using (3), (4) and (5) they obtained
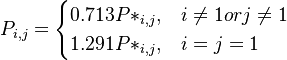
with
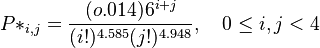 .
.
The estimated parameters are: a = b = 6, k = 4.585, m = 4.948, α = 0.713, β = 1.291, 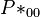 = 0.014, N = 610 and the fitting is presented in Table 2. For example
= 0.014, N = 610 and the fitting is presented in Table 2. For example 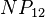 is computed as
is computed as
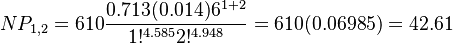 .
.
The result is acceptable without testing.
4. Authors: U. Strauss, G. Altmann
5. References
Lee, Sank-Oak (1986). An explanation of syllable structure change. Korean Language Research 22, 195-213.
Vennemann, T. (1982) (ed.). Zur Silbenstruktur der deutschen Standardsprache. Silben, Segmente, Akzente: 261-305. Tübingen: Narr.
Zörnig, P., Altmann, G. (1993). A model for the distribution of syllable types. Glottometrika 14, 190-196.