Difference between revisions of "Morph length"
m |
|||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
Morph length is a specal case of length or word length (<math>\rightarrow</math>) research. The segmentation of a text in morphs is a problem depending on language and grammar (cf. Best 2001 for German). | Morph length is a specal case of length or word length (<math>\rightarrow</math>) research. The segmentation of a text in morphs is a problem depending on language and grammar (cf. Best 2001 for German). | ||
Morph lengths are focussed in Quantitative Linguistics in different ways: | Morph lengths are focussed in Quantitative Linguistics in different ways: | ||
| − | Gerlach (1982) tested the interaction of word length with morph length in a German lexicon; the hypothesis was: the more | + | Gerlach (1982) tested the interaction of word length with morph length in a German lexicon; the hypothesis was: the more morphs a word has, the shorter the morphs are. The test results were very good. Without any data Saporta (1963: 70) proposes the hypothesis: “The mean length of morphs will be inversely related to the number of phonemes in the inventory.” This idea is said to go back to R. Jakobson (Saporta 1963: 72, footnote 15). |
| − | Here we are confronted with another hypothesis: morph lengths in texts abide by a law the same way as word lengths and other entities do. | + | Here we are confronted with another hypothesis: morph lengths in texts abide by a law in the same way as word lengths and other entities do. |
Since up to now only a small number of data has been collected (Best 2000a, 2001a) the only distribution found rather inductively but belonging to the family of length-distributions (cf. Wimmer, Altmann 1996) was the 1-displaced Hyperpoisson distribution. | Since up to now only a small number of data has been collected (Best 2000a, 2001a) the only distribution found rather inductively but belonging to the family of length-distributions (cf. Wimmer, Altmann 1996) was the 1-displaced Hyperpoisson distribution. | ||
In a paper concerning morph segmentation Creutz (2003: 282) proposes the gamma distribution to be a model for morph lengths in the lexicon; but there is no proof of it. As soon as 1963 Saporta (²1966: 69) presents a little overview over morph lengths (in phonemes) in Spanish; testing the data (1679 morphs) the binomial distribution can be shown to be an acceptable model (C = 0.0166). He “cannot help wondering whether or not such a distribution is universal and, if not, what other factors correlate with different distributions.” | In a paper concerning morph segmentation Creutz (2003: 282) proposes the gamma distribution to be a model for morph lengths in the lexicon; but there is no proof of it. As soon as 1963 Saporta (²1966: 69) presents a little overview over morph lengths (in phonemes) in Spanish; testing the data (1679 morphs) the binomial distribution can be shown to be an acceptable model (C = 0.0166). He “cannot help wondering whether or not such a distribution is universal and, if not, what other factors correlate with different distributions.” | ||
| Line 11: | Line 11: | ||
'''2. Hypothesis''' | '''2. Hypothesis''' | ||
| − | ''2.1. Morph length in texts abides by a regular probability distribution derived form the unified theory, namely the 1-displaced Hyperpoisson distribution. | + | ''2.1. Morph length in texts abides by a regular probability distribution derived form the unified theory, namely the 1-displaced Hyperpoisson distribution.'' |
| − | 2.2. If morphs have specific forms, the distribution is multimodal and must be modeled by an appropriate approach''. | + | |
| + | ''2.2. If morphs have specific forms, the distribution is multimodal and must be modeled by an appropriate approach''. | ||
'''3. Derivation''' | '''3. Derivation''' | ||
| Line 24: | Line 25: | ||
Best (2001a) used a text from Eichsfelder Tageblatt (6.3.1997, p.8): „Sieben Deutsche in Jemen entführt)“ and counting the length of morphemes he obtained the results in Table 1. | Best (2001a) used a text from Eichsfelder Tageblatt (6.3.1997, p.8): „Sieben Deutsche in Jemen entführt)“ and counting the length of morphemes he obtained the results in Table 1. | ||
| − | <div align="center">[[Image: | + | <div align="center">[[Image:Tabelle111_ML.jpg]]</div> |
| + | |||
<div align="center">[[Image:Grafik1_ML.jpg]]</div> | <div align="center">[[Image:Grafik1_ML.jpg]]</div> | ||
| Line 31: | Line 33: | ||
| − | 3.2. In Lakota morphemes usually consist of even number of syllables. In that case the usual approach must be extended and the distribution must be modeled by a difference equation of second order i.e. | + | 3.2. In Lakota, morphemes usually consist of even number of syllables. In that case the usual approach must be extended and the distribution must be modeled by a difference equation of second order i.e. |
| − | (2)<math> P_x = g(x)P_{x-1}+h(x)P_{x-2}\quad</math>. | + | (2)<math> P_x = g(x)P_{x-1}+h(x)P_{x-2}\quad</math>. |
Pustet and Altmann (2005) set g(x) = a(k + x – 1)/x and h(x) = b(2k + x – 2)/x and obtained as solution the Gegenbauer distribution given as | Pustet and Altmann (2005) set g(x) = a(k + x – 1)/x and h(x) = b(2k + x – 2)/x and obtained as solution the Gegenbauer distribution given as | ||
| Line 39: | Line 41: | ||
(3)<math> P_x = (n)=\begin{cases} (1-a-b)^k,\quad x=0 \\ p_0 \sum_{j=0}^{[x/2]}\frac{b^j k^{(x-j)}a^{x-2j}}{j!(x-2j)!}, \quad x = 1, 2, 3,...\end{cases} </math> | (3)<math> P_x = (n)=\begin{cases} (1-a-b)^k,\quad x=0 \\ p_0 \sum_{j=0}^{[x/2]}\frac{b^j k^{(x-j)}a^{x-2j}}{j!(x-2j)!}, \quad x = 1, 2, 3,...\end{cases} </math> | ||
| − | where [.] is the integer part and k(x - j) is the ascending factorial function. | + | where [.] is the integer part and k<sup>(x - j)</sup> is the ascending factorial function. |
'''Example'''. Morpheme length in Lakota | '''Example'''. Morpheme length in Lakota | ||
| − | Pustet and Altmann (2005) modeled the morpheme distribution in Lakota and obtained the results in Table 2 and Fig. 2. | + | Pustet and Altmann (2005) modeled the morpheme length distribution in Lakota and obtained the results in Table 2 and Fig. 2. |
| − | <div align="center">[[Image: | + | <div align="center">[[Image:Tabelle222_ML.jpg]]</div> |
<div align="center">[[Image:Grafik2_ML.jpg]]</div> | <div align="center">[[Image:Grafik2_ML.jpg]]</div> | ||
| Line 51: | Line 53: | ||
| − | '''4. Authors: G. Altmann, K.-H. Best''' | + | '''4. Authors: U. Strauss, G. Altmann, K.-H. Best''' |
'''5. References''' | '''5. References''' | ||
| Line 58: | Line 60: | ||
'''Best, K.-H'''. (2001a). Zur Länge von Morphen in deutschen Texten. In: Best, K.-H. (ed.), ''Häufigkeitsverteilungen in Texten: 1-14''. Göttingen: Peust & Gutschmidt. | '''Best, K.-H'''. (2001a). Zur Länge von Morphen in deutschen Texten. In: Best, K.-H. (ed.), ''Häufigkeitsverteilungen in Texten: 1-14''. Göttingen: Peust & Gutschmidt. | ||
| + | |||
| + | '''Best, K.-H.''' (2001b). Probability distributions of language entities. ''J. of Quantitative Linguistics 8, 1-11.'' | ||
'''Best, K.-H'''. (2005). Morphlänge. In: Köhler, R., Altmann, G., Piotrowski, R. (eds.), ''Quantitative Linguistik - Quantitative Linguistics. Ein internationales Handbuch: 255-260''. Berlin/ N.Y.: de Gruyter | '''Best, K.-H'''. (2005). Morphlänge. In: Köhler, R., Altmann, G., Piotrowski, R. (eds.), ''Quantitative Linguistik - Quantitative Linguistics. Ein internationales Handbuch: 255-260''. Berlin/ N.Y.: de Gruyter | ||
| Line 65: | Line 69: | ||
'''Gerlach, R.''' (1982). Zur Überprüfung des Menzerathschen Gesetzes im Bereich der Morphologie. ''Glottometrika 4, 95-102''. | '''Gerlach, R.''' (1982). Zur Überprüfung des Menzerathschen Gesetzes im Bereich der Morphologie. ''Glottometrika 4, 95-102''. | ||
| − | '''Gorot´, E.I.''' (1990). Izomorfnye i otličitel´nye čerty morfemy i sloga v raspredelenii dliny. In: | + | '''Gorot´, E.I.''' (1990). Izomorfnye i otličitel´nye čerty morfemy i sloga v raspredelenii dliny. In: ''Kvantitativnaja lingvistika i avtomatičeskij analiz tekstov: 32-36''. Tartu. |
'''Krott, A'''. (1996). Some remarks on the relation between word length and morpheme length. ''J. of Quantitative Linguistics 3, 29-37''. | '''Krott, A'''. (1996). Some remarks on the relation between word length and morpheme length. ''J. of Quantitative Linguistics 3, 29-37''. | ||
| Line 77: | Line 81: | ||
'''Wimmer, G., Altmann, G'''. (1996). The theory of word length: some results and generalizations. ''Glottometrika 15, 112-133''. | '''Wimmer, G., Altmann, G'''. (1996). The theory of word length: some results and generalizations. ''Glottometrika 15, 112-133''. | ||
| − | + | ||
| − | + | [[Category:Unfertig]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 11:05, 26 January 2012
1. Problem and history
Morph length is a specal case of length or word length (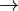 ) research. The segmentation of a text in morphs is a problem depending on language and grammar (cf. Best 2001 for German).
Morph lengths are focussed in Quantitative Linguistics in different ways:
Gerlach (1982) tested the interaction of word length with morph length in a German lexicon; the hypothesis was: the more morphs a word has, the shorter the morphs are. The test results were very good. Without any data Saporta (1963: 70) proposes the hypothesis: “The mean length of morphs will be inversely related to the number of phonemes in the inventory.” This idea is said to go back to R. Jakobson (Saporta 1963: 72, footnote 15).
Here we are confronted with another hypothesis: morph lengths in texts abide by a law in the same way as word lengths and other entities do.
Since up to now only a small number of data has been collected (Best 2000a, 2001a) the only distribution found rather inductively but belonging to the family of length-distributions (cf. Wimmer, Altmann 1996) was the 1-displaced Hyperpoisson distribution.
In a paper concerning morph segmentation Creutz (2003: 282) proposes the gamma distribution to be a model for morph lengths in the lexicon; but there is no proof of it. As soon as 1963 Saporta (²1966: 69) presents a little overview over morph lengths (in phonemes) in Spanish; testing the data (1679 morphs) the binomial distribution can be shown to be an acceptable model (C = 0.0166). He “cannot help wondering whether or not such a distribution is universal and, if not, what other factors correlate with different distributions.”
However, in Lakota the morphs have a specific form and their frequency distribution must be modelled by means of a difference equation of second order.
) research. The segmentation of a text in morphs is a problem depending on language and grammar (cf. Best 2001 for German).
Morph lengths are focussed in Quantitative Linguistics in different ways:
Gerlach (1982) tested the interaction of word length with morph length in a German lexicon; the hypothesis was: the more morphs a word has, the shorter the morphs are. The test results were very good. Without any data Saporta (1963: 70) proposes the hypothesis: “The mean length of morphs will be inversely related to the number of phonemes in the inventory.” This idea is said to go back to R. Jakobson (Saporta 1963: 72, footnote 15).
Here we are confronted with another hypothesis: morph lengths in texts abide by a law in the same way as word lengths and other entities do.
Since up to now only a small number of data has been collected (Best 2000a, 2001a) the only distribution found rather inductively but belonging to the family of length-distributions (cf. Wimmer, Altmann 1996) was the 1-displaced Hyperpoisson distribution.
In a paper concerning morph segmentation Creutz (2003: 282) proposes the gamma distribution to be a model for morph lengths in the lexicon; but there is no proof of it. As soon as 1963 Saporta (²1966: 69) presents a little overview over morph lengths (in phonemes) in Spanish; testing the data (1679 morphs) the binomial distribution can be shown to be an acceptable model (C = 0.0166). He “cannot help wondering whether or not such a distribution is universal and, if not, what other factors correlate with different distributions.”
However, in Lakota the morphs have a specific form and their frequency distribution must be modelled by means of a difference equation of second order.
2. Hypothesis
2.1. Morph length in texts abides by a regular probability distribution derived form the unified theory, namely the 1-displaced Hyperpoisson distribution.
2.2. If morphs have specific forms, the distribution is multimodal and must be modeled by an appropriate approach.
3. Derivation
3.1. Substituting 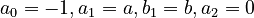 in formula (10) of unified theory (→) and solving with displacement one obtains the Hyperpoisson distribution
in formula (10) of unified theory (→) and solving with displacement one obtains the Hyperpoisson distribution
(1)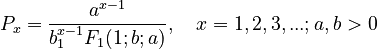
Example: Morph length distribution in German
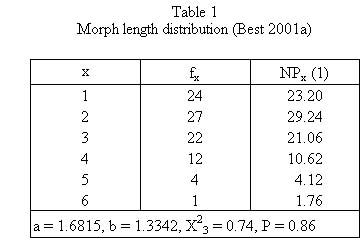
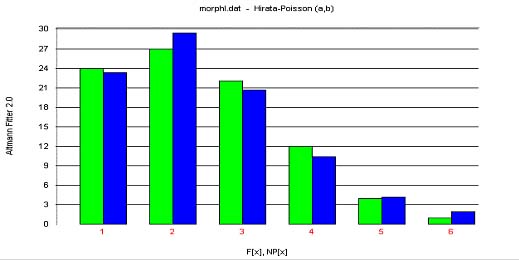
Best (2001a) used a text from Eichsfelder Tageblatt (6.3.1997, p.8): „Sieben Deutsche in Jemen entführt)“ and counting the length of morphemes he obtained the results in Table 1.
3.2. In Lakota, morphemes usually consist of even number of syllables. In that case the usual approach must be extended and the distribution must be modeled by a difference equation of second order i.e.
(2)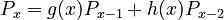 .
.
Pustet and Altmann (2005) set g(x) = a(k + x – 1)/x and h(x) = b(2k + x – 2)/x and obtained as solution the Gegenbauer distribution given as
(3)![P_x = (n)=\begin{cases} (1-a-b)^k,\quad x=0 \\ p_0 \sum_{j=0}^{[x/2]}\frac{b^j k^{(x-j)}a^{x-2j}}{j!(x-2j)!}, \quad x = 1, 2, 3,...\end{cases}](/images/math/6/f/d/6fd95493a14ff9ea717624d3ceff8cc3.png)
where [.] is the integer part and k(x - j) is the ascending factorial function.
Example. Morpheme length in Lakota
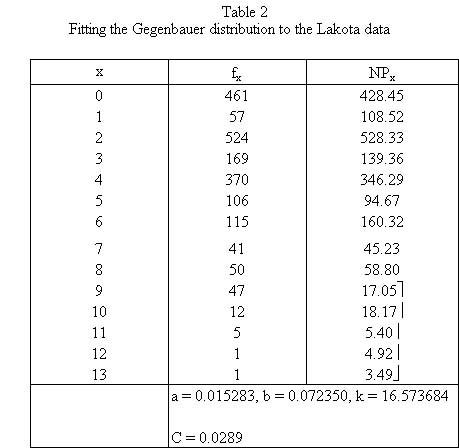
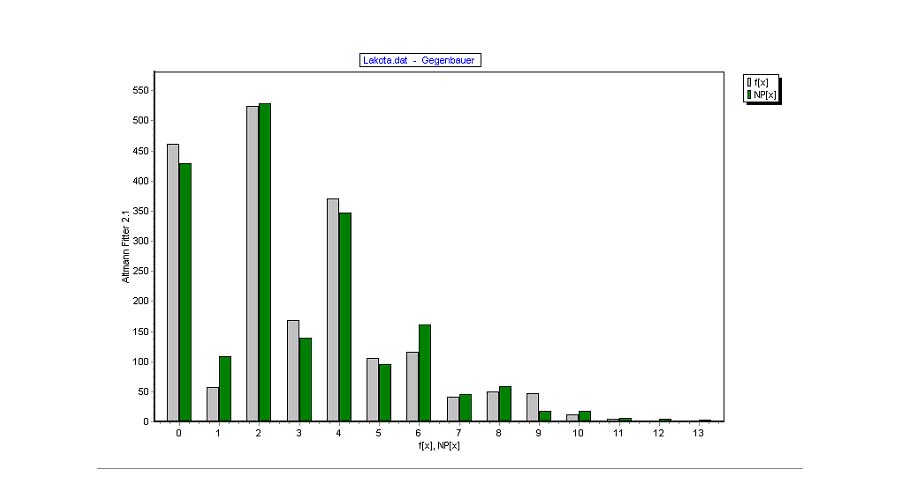
Pustet and Altmann (2005) modeled the morpheme length distribution in Lakota and obtained the results in Table 2 and Fig. 2.
4. Authors: U. Strauss, G. Altmann, K.-H. Best
5. References
Best, K.-H. (2000a). Morphlängen in Fabeln von Pestalozzi. Göttinger Beiträge zur Sprachwissenschaft 3, 19-30.
Best, K.-H. (2001a). Zur Länge von Morphen in deutschen Texten. In: Best, K.-H. (ed.), Häufigkeitsverteilungen in Texten: 1-14. Göttingen: Peust & Gutschmidt.
Best, K.-H. (2001b). Probability distributions of language entities. J. of Quantitative Linguistics 8, 1-11.
Best, K.-H. (2005). Morphlänge. In: Köhler, R., Altmann, G., Piotrowski, R. (eds.), Quantitative Linguistik - Quantitative Linguistics. Ein internationales Handbuch: 255-260. Berlin/ N.Y.: de Gruyter
Creutz, M. (2003). Unsupervised segmentation of words using prior distributions of morph length and frequency. Proceedings of ACL-03, The 41st Annual Meeting of th Association of Computational Linguistics: 280-287. Sapporo, Japan, 7-12 July.
Gerlach, R. (1982). Zur Überprüfung des Menzerathschen Gesetzes im Bereich der Morphologie. Glottometrika 4, 95-102.
Gorot´, E.I. (1990). Izomorfnye i otličitel´nye čerty morfemy i sloga v raspredelenii dliny. In: Kvantitativnaja lingvistika i avtomatičeskij analiz tekstov: 32-36. Tartu.
Krott, A. (1996). Some remarks on the relation between word length and morpheme length. J. of Quantitative Linguistics 3, 29-37.
Nikonov, V.A. (1978). Dlina slova. Voprosy jazykoznanija 6, 104-111.
Pustet, R., Altmann, G. (2005). Morpheme length distribution in Lakota. J. of Quantitative Linguistics 12(1), 53-63.
Saporta, S. (1963, ²1966). Phoneme distribution and language universals. In: Greenberg, J.H. (ed.), Universals of language. Second edition. Report of a conference held at Dobbs Ferry, New York, April 13-115, 1961: 61-72. Cambridge, Mass. & London: The M.I.T. Press.
Wimmer, G., Altmann, G. (1996). The theory of word length: some results and generalizations. Glottometrika 15, 112-133.