Difference between revisions of "Position of syntactic structures"
| Line 29: | Line 29: | ||
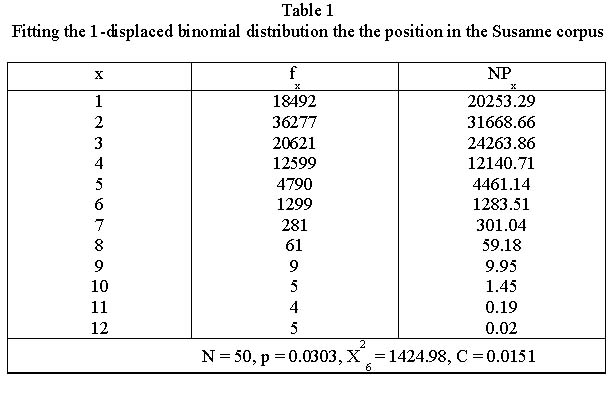
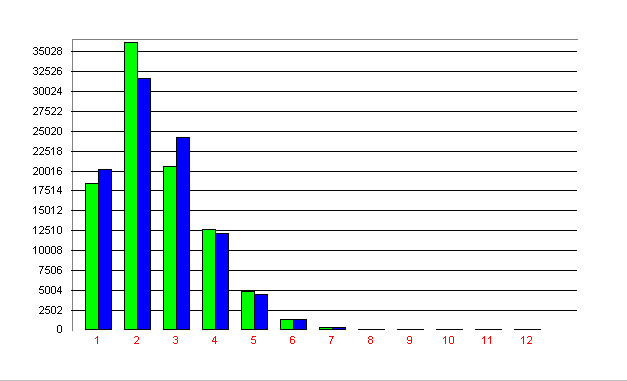
Köhler and Altmann futted to these data the 1-displaced binomial distribution and obtained the results presented in Table 1 and Fig. 1. | Köhler and Altmann futted to these data the 1-displaced binomial distribution and obtained the results presented in Table 1 and Fig. 1. | ||
| − | |||
| − | |||
| + | <div align="center">[[Image:Tabelle11_PoSS.jpg]]</div> | ||
<div align="center">[[Image:Grafik2_PoSS.jpg]]</div> | <div align="center">[[Image:Grafik2_PoSS.jpg]]</div> | ||
Revision as of 10:30, 29 June 2006
1. Problem and history
According to Köhler (1999) the number of allowed constituent types and functions decreases with increasing position in the construct because the necessary storage space in the memory increases from position to position. Thus the number of constituents in a corpus located at individual positions x (x = 1,2,3,…) must follow a specific regularity. The problem was tackled for the first time by Köhler (1999), the probability distribu-tion was derived by Köhler and Altmann (2000).
2. Hypothesis
The number of constituents at given positions follows the binomial distribution.
3. Derivation
The quantities necessary for the derivation are the same as with complexity ( Complexity of syntactic structures). However, here complexity is implicit (the complexity of a constituent is its maximum position), thus minX = 0. The compactness maxH is constant and can be written as n+1. Since increasing the position decreases the probability, x in the numerator has negative sign. Setting p/q for E/I(K) and taking the displacement into account (there is no position 0) we obtain
(1)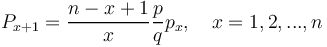
resulting in the 1-displaced binomial distribution
(2)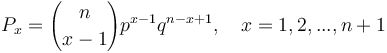 .
.
Since there are also data displaying bimodal course (e.g. the Negra-Korpus), formula (2) can be modified as follows (P’x = parent 1-displaced binomial distribution)
(3)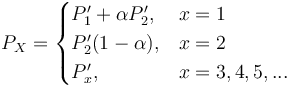
resulting in the Cohen-binomial distribution
(4)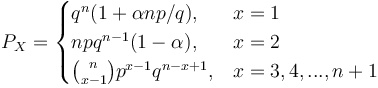
Example: Distribution of the position in the Susanne corpus Köhler and Altmann futted to these data the 1-displaced binomial distribution and obtained the results presented in Table 1 and Fig. 1.
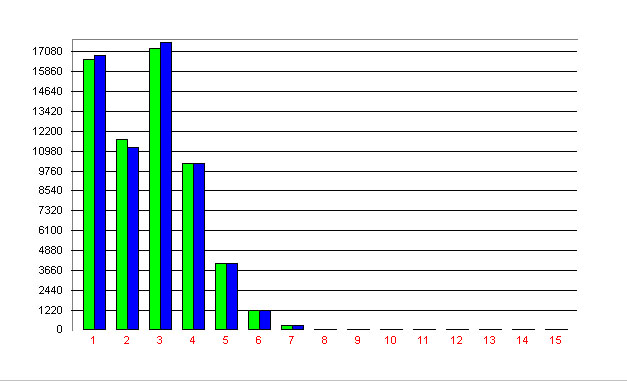
Example: Distribution of the position in the Negra-Korpus
Köhler and Altmann fitted the Cohen-binomial distribution to the Negra-Korpus and obtained the results in Table 2 and Fig. 2.
Table 2 Fitting the Cohen-Binomial distribution to the Negra-Korpus
4. Authors: G. Altmann
5. References
Köhler, R. (1999). Syntactic structures: Properties and interrelations. J. of Quantitative Linguistics 6, 46-57.
Köhler, R., Altmann, G. (2000). Probability distributions of syntactic units and properties. J. of Quantitative Linguistics 7, 189-200.