Morph polysemy and morph inventory
1. Problem and history
The hypothesis on the relation between these two entities states that the richer the mean polysemy of morphs, the smaller the inventory of morphs. If the existing morphs cover the necessary universe of discourse, then there is no need to increase their inventory. The problem is part of synergetic linguistics and was elaborated by A. Krott (2002), who brought several hypotheses about morphs analogous to those of words. As far as known there are no further works. The author tested the hypothesis on CELEX data but did not bring numerical results. In systems theoretical terms the inventory size of morphs depends on the extent of polysemy of existing morphs, with which two requirements interact: the need for coding (COD) having a positive effect C, and the requirement for minimum inventory minI having a negative effect S. Since in synergetic linguistics one works with logarithmically transformed values, one can write this relationship as
(1) 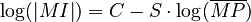 .
.
Here
MI = morpheme inventory,
|MI| = size of morpheme inventory
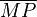 = mean morph polysemy
= mean morph polysemy
or displayed in systems theoretical terms
[[[Bild 2.1.3 in Krott, S. 78. Die Inschriften wie folgt ändern: Kod Þ Cod L-ÆMorph-Polysemie Þ log( ) oder L(Mean Morph Polysemy) oder beide L-Morph-Inv.-Umfang Þ log(|MI|) oder L(Morph Inventory Size) oder beide]]]
Fig. 1. Dependence of morph inventory size on morph polysemy (Krott 2002)
For other hypotheses on morphs see ……………………
2. Hypothesis
The relative rate of change of the size of morph inventory (y) is inversely proportional to the mean morph polysemy (x).
3. Derivation
(2)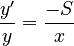
yielding
(3)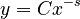
where the integration constant is interpreted as he coding requirement and the proportionality constant as the constant need for inventory minimisation.
Example: Not at disposal (Krott finden!!!)
4. Authors: R. Köhler, G. Altmann, J. Eom
5. References
Krott, A. (2002). Ein funktionalanalytisches Modell der Wortbildung. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 75-126. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/