Frequency and polytextuality
1. Problem and history
Under polytextuality one understands the number of environments of a linguistic entity. The entity can be syllable, mora, morphem, word and other units. The environment for syllable, mora and morphem is the word, the environment of the word are other words. Usually the number of different environments is called number of types. The frequency of the given entity in all its environments in, say, a corpus, is considered as the number of tokens. The question is, whether there is some relationship between the number of types (environments) and the number of tokens (frequency) of units of the given level.
The relationship between frequency and polytextuality has been launched by R. Köhler (1986) as a complement to Zipfian properties, in order to enlarge his control cycle. Since the computation of data is very laborious and the erroneous identification with another “type-token” problem ( ) lead to confusion, one can find this relationship also under the name “(morphological) productivity” (cf. Baayen 2001) which in turn represents a slightly different problem (cf. Wimmer, Altmann 1995). The relationship appeared in different works on language synergetics (cf. e.g. Gieseking 2002), Köhler (2005) reformulated the pertinent part of his control cycle and Tamaoka, Altmann (2005) showed by means of Japanese morae that the unified theory (
) lead to confusion, one can find this relationship also under the name “(morphological) productivity” (cf. Baayen 2001) which in turn represents a slightly different problem (cf. Wimmer, Altmann 1995). The relationship appeared in different works on language synergetics (cf. e.g. Gieseking 2002), Köhler (2005) reformulated the pertinent part of his control cycle and Tamaoka, Altmann (2005) showed by means of Japanese morae that the unified theory ( ) leads to the identical result.
) leads to the identical result.
Usually one considers frequency as the spiritus movens, the independent variable of many relationships, but Köhler (1986) assumed here an inverse relationship.
2. Hypothesis
The frequency of linguistic units depends on their polytextuality.
3. Derivation
Since in most cases linguistic properties are related by their relative rates of change, Tamaoka and Altmann (2005), taking into account some ceteris paribus factors, and leaning against the unfied theory ( ) set up the equation
) set up the equation
(1)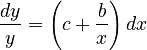
where x is polytexty, y is frequency and c are some additional factors. They considered Japanese morae, their polytexty and frequency in a Japanese corpus. The resulting equation is
(2)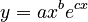 .
.
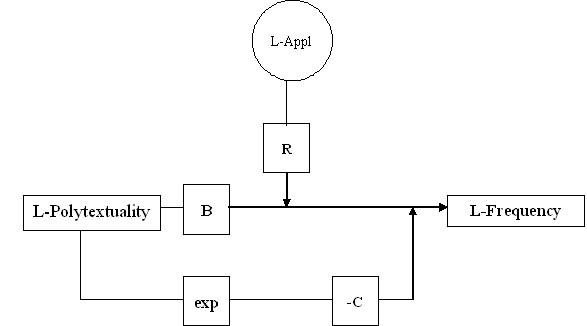
Using Köhlers model (Fig. 1) one can write the relationships as follows:
(3) ln(F) = R ln(Appl) + B ln(PT) – C exp(ln(PT))
i.e. ln(F) = R ln(Appl) + B ln(PT) – C (PT)\quad
from which
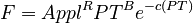
follows. Since 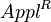 can, in the framework of a synchronic study, be considered as a constant, say A, PT = x, and F = y, we obtain
can, in the framework of a synchronic study, be considered as a constant, say A, PT = x, and F = y, we obtain
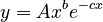
whih is identical with the above result of the differential equation.
Fig. 1. The relationship between polytextuality and frequency in general
Thus Köhler´s model explains also the additional factors.
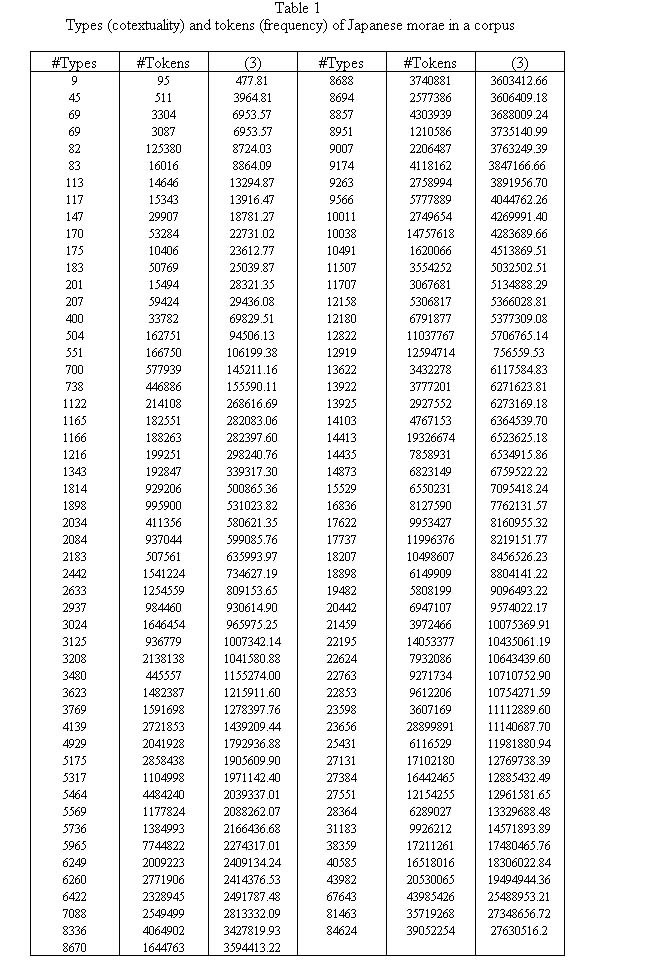
Example 1. Types and token of Japanese morae
Tamaoka and Makioka (2004) computed the frequencies of 103 Japanese morae in a corpus containing 341,771 different words with total frequency 287,792,797. For each mora its frequency and the contexts (different words) were ascertained. Tamaoka and Altmann (2005) showed that the best fit to these data (in logarithmic transformation) can be obtained by the curve
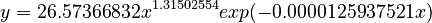 .
.
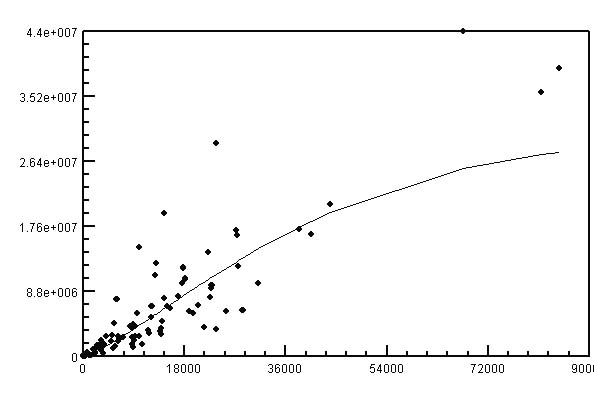
yielding a determination coeffciient D = 0.92. The result of fitting is displayd in Table 1 and graphically presented in Fig. 2.
4. Authors: R. Köhler, G. Altmann
5. References
Baayen, R.H. (2001). Word frequency distributions. Dordrecht: Kluwer.
Gieseking, K. (2002). Untersuchungen zur Synergetik der englischen Lexik. In: Köhler, R. (ed.), Korpuslinguistische Untersuchungen in die quantitative und systemtheoretische Linguistik: 387-433. http://ubt.opus.hbz-nrw.de/volltexte/2004/279/
Köhler (2005)………….
Tamaoka, K., Altmann, G. (2005). On the relation between types and tokens of Japanese morae………….
Tamaoka, K., Makioka, Sh. (2004). Frequency of occurrence for units of phonemes, morae, and syllables appearing in a lexical corpus of a Japanese newspaper. Behavior Research Methods, Instruments & Computers 36(3), 531-547.
Wimmer, G., Altmann, G. (1995). A model of morphological productivity. J. of Quantitative Linguistics 2, 212-216.