Syllable length

1. Problem and history

The problem is to find the distribution of syllable length measured in terms of letter, phone or phoneme numbers. It is connected with the general problem of length ($\rightarrow$). Another problem is that of syllable duration which was considered merely in connection with hierarchic relations ($\rightarrow$). The research is very young, it began in the Göttingen Project with works by Zuse (1998) and Cassier (1998), up to now further tests have been performed merely by Best (2001b), Rottmann (1999, 2002) and Schneemann (2001).

2. Hypothesis

Syllable length abides by a regular distribution following from the unified theory ($\rightarrow$).

3. Derivation

Since there are no zero-phoneme syllables, one solves the formulas of the “length approach” for the displaced case, namely

(1)$P_{x+1} = g(x)P_x, \quad x=1, 2, 3, ...$.

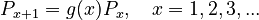Up to now only three different cases have been observed:

3.1. The 1-displaced hyperbinomial distribution (Rottmann 1999)

Substituting in (1)

$g(x) = \frac{q(n-x+1)}{m+x-1}$

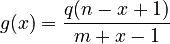
one obtains the 1-displaced hyperbinomial distribution

(2) $P_x = \frac{{n \choose x-1}}{{m+x-2 \choose x-1}}q^{x-1}P_1, x= 1, 2, 3, ..., n; m>0, n \epsilon N, 0<q<1$

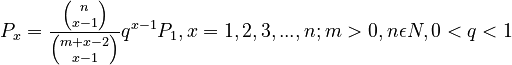
P1 being the norming constant 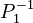$P_1^{-1}$ (see Appendix). It is a special case of the unified theory (11) when $1+ a_0 = -q, a_1 = q(m+n), a_2 = 0, b_1= m-1, c_1 = 1$.

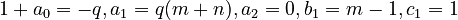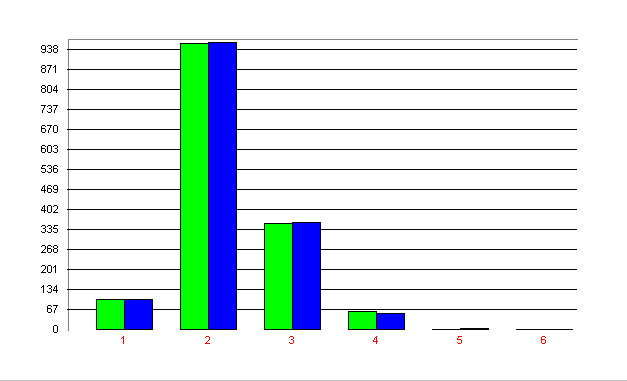
Example: Syllable length in East Slavonic

Rottmann (1999) examined the syllable length in East Slavonic texts. One of his results is presented in Table 1 and Fig. 1.

Fig. 1. Fitting the 1-displaced hyperbinomial distribution to the data in Table 1

3.2. The 1-displaced Conway-Maxwell-Poisson distribution (Cassier 1998, Best 2001b)

Substituting in (1)

$g(x) = \frac{a}{x^b}$

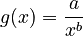
one obtains the 1-displaced Conway-Maxwell-Poisson distribution

(3)$P_x = \frac{Ca^{x-1}}{(x-1)!^b}, \quad x= 1, 2, 3, ...; a, b >0$,

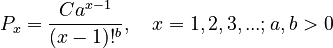wehere C is the normalizing constant 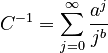$C^{-1} = \sum_{j=0}^\infty \frac{a^j}{j^b}$ . It is a special case of the unified theory, formula (11) when $a_0 = -1, a_1 = a, b_1 = a_2 = a_3 = ... = 0, c_1 = b$.

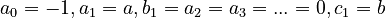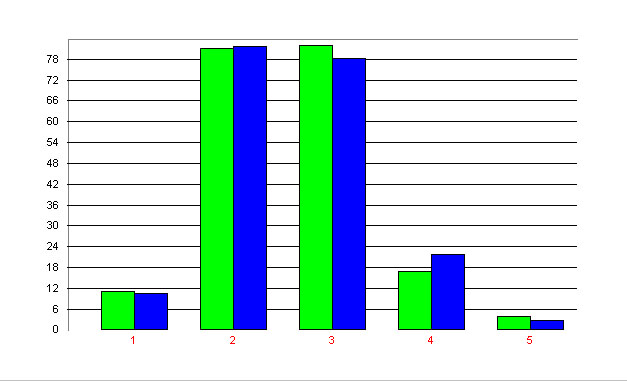
Example: Syllable length in German

Best (2001b) examined syllable length in 21 German journalistic texts. In text 5 he obtained the results presented in Table 2 and Fig. 2.

Fig. 2. Fitting the 1-displaced Conway-Maxwell-Poisson distribution to the data in Table 2

3.3. The positive Cohen-Poisson distribution (Zuse 1998, Rottmann 1999)

If the first class is modified such that

$P_1 = (1-\alpha)C\quad$

$P_2 = \frac{a}{2}C$

$P_x = \frac{a}{x}P_{x-1}, \quad x=2, 3, 4, ...$

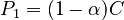
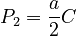
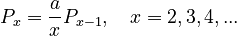
then one obtains the positive Cohen-Poisson distribution

(4)$P_x = f(n)=\begin{cases} \frac{(1-a\alpha}{e^{-a}-1-a\alpha}, & x=1 \\ \frac{a^x}{x!(e^{-a}-1-a\alpha}, & x=2,3,4... \end{cases}$

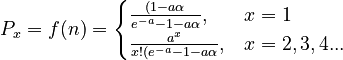
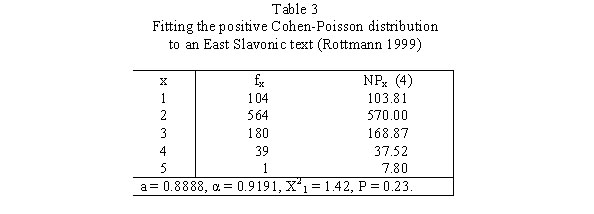
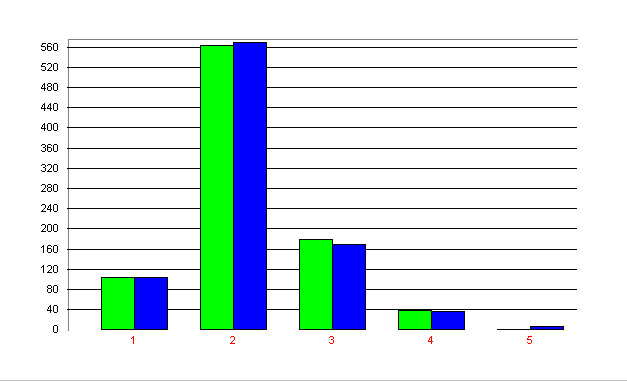
Example: Syllable length in East Slavonic

Rottmann (1999) fitted the positive Cohen-Poisson distribution to East Slavonic texts and in three cases where the hyperbinomial distribution was not adequate he obtained satisfactory results. Table 3 and Fig. 3. Show one of the fittings.

Fig. 3. Fitting the positive Cohen-Poisson distribution to the data in Table 3.

4. Authors: G. Altmann, K.-H. Best

5. References

Best, K.-H. (2001b). Silbenlängen in Meldungen der Tagespresse. In: Best, K.H. (ed.), Häufigkeitsverteilungen in Texten: 15-32. Göttingen: Peust & Gutschmidt.

Cassier, F.U. (1998). Silbenlängen in Meldungen der deutschen Tagespresse. Göttingen: Staatsexamensarbeit.

Cassier, F.U. (2001). Silbenlängen in Meldungen der deutschen Tagespresse. In: Best, K.H. (ed.), Häufigkeitsverteilungen in Texten: 33-42. Göttingen: Peust & Gutschmidt.

Gorot´, E.I. (1990). Izomorfnye i otličitel´nye čerty morfemy i sloga v raspredelenii dliny. In: Kvantitativnaja lingvistika i avtomatičeskij analiz tekstov: 32-36. Tartu.

Kučera, H. (1963). Entropy, redundancy and functional load in Russian and Czech. In: American Contributions to the Fifth International Cobgress of Slavists: 191-219. The Hague: Mouton.

Ludvíková, M. (1977). On some statistical differences in two spoken texts on the syllabic level. Prague Studies in Matgematical Linguistics 5, 91-104.

Malécot, A., Johnston, R., Kizziar, R.A. (1972). Syllabic rate and utterance length in French. Phonetica 26, 35-261.

Rottmann, O. A. (1999). Word and syllable lengths in East Slavonic. J. of Quantitative Linguistics 6: 235-238.

Rottmann, O. A. (2002) Syllable length in Russian, Bulgarian, Old Church Slavonic and Slovene. Glottometrics 2: 87-94.

Rykov, V. (1994). Menzerath law for printed speech. In: 2nd International Conference on Quantitative Linguistics, September 20-24, 1994, Moscow: 199-200. Moscow: Lomonosov Moscow State University.

Schneemann, O. F. (2001). Sprachstatistische Untersuchungen zu Wort- und Silbenlängen in deutschen Musikzeitschriften. Staatsexamensarbeit, Göttingen.

Zuse, M. (1998). Silbenlängen in deutschen und englischen Pressetexten der Gegenwart. Göttingen: Staatsexamensarbeit.