Syllable structure

1. Problem and history

If syllables are coded in the canonical form, V, CV, CVC, etc. where the vowel (V) is the syllable nucleus and the consonant (C) is the periphery, we obtain a set of structural types whose number follows a specific two-dimensional distribution. The types can be presented in tabular form

V VC VCC VCCC … Vs V CV CCV CCCV … rV n00 n01 no2 n03 … n0s n10 n11 n12 n13 … n1s n20 n21 n22 n23 … n2s n30 n31 n32 n33 … n3s … … … … … … nr0 nr1 nr2 nr3 … nrs

Where the frequency of the type CVVCC is given as n12, i symbolizing the number of consonants before and j that behind the nucleus. There are at most r onsets and s codas in the syllable. Let 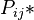$P_{ij}*$ be the corresponding probability.

2. Hypothesis

The distribution of canonical syllable types abides by the (modified) bivariate Conway-Maxwell-Poisson distribution.

3. Derivation

Starting from the unified theory we assume that the probabilities of syllable types are joined with the following proportionality relation

(1)$P_{i,j}* P_{i, j-1}*$ $P_{i,j}* P_{i-1, j}*$

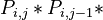
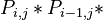
i.e. a class is proportional to its left or upper neighbour. In the first step Zörnig and Altmann (1993) used the simple Menzerathian relatioship (see Hierarchic relations) as proprotionality function and obtained

(2)$P_{i,j}* = \frac{b}{j^m}P_{i, j-1}*$ $P_{i,j}* = \frac{a}{i^k}P_{i-1, j}*, \quad m,k \epsilon \mathfrak{R}$

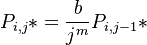
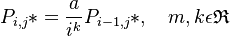
The solution of (2) yields

(3)$P_{i,j}* = \frac{a^1 b^j}{(i!)^k (j!)^m}P_{0,0}*, \quad i= 0,1,...,r, \quad j=0,1,...,s$

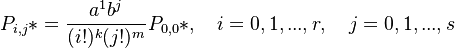
where the norming constant is 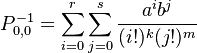$P_{0,0}^{-1} = \sum_{i=0}^r \sum_{j=0}^s\frac{a^i b^j}{(i!)^k(j!)^m}$ .

Since the particular case examined (Indonesian) has a strong preference for the CVC type ( = 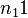$n_11$) the distribution must be modified and renormed. Weighting 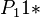$P_11*$ by β the other probabilities must be weighted so that 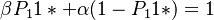$\beta P_11* + \alpha(1-P_11*) = 1$. As a result we obtain

(4)$P_{i,j}= \begin{cases} \beta P_{i,j}*, & i=j=1 \\ \alpha P_{i,j}*, & i= 0,1,...,r,\quad j=0,1,...,s,\quad i \ne 1 or j \ne 1\end{cases}$

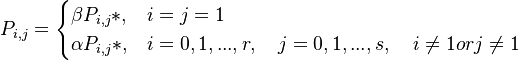
Zörnig and Altmann (1993) show also the estimators won from frequency classes as

(5)$\hat a = n_{10} / n_{00}$

$\hat b = n{01}/n_{00}$

$\hat k \ln(\hat a n_{10}/n_{20})$

$\hat m \ln(\hat b n_{01}/n_{02})$

$\hat \alpha = 1+ \frac{n_{10}\hat b - n_{11}}{N}$

$\hat \beta = \hat \alpha n_{11} /(n_{10}\hat b)$

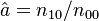
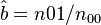
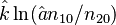
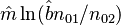
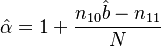
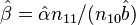
Example. Structure of Indonesian syllables

In about 15000 Indonesian word forms from different texts Zörnig and Altmann (1993) found 610 syllable types shown in Table 1.

Table 1 Indonesian syllable types

V VC VCC VCCC V CV CCV CCCV 6 36 7 - 36 391 44 2

 9	  61	13	   -
 1	    4	  -	   -

Using (3), (4) and (5) they obtained

with .

The estimated parameters are: a = b = 6, k = 4.585, m = 4.948, α = 0.713, β = 1.291, P*00 = 0.014, N = 610 and the fitting is presented in Table 2. For example NP12 is computed as

.

Table 2 Fitting (3) and (4) to Indonesian data (Zörnig, Altmann 1993)

0 1 2 3 0 1 2 3 6.1 36.5 7.1 0.2 36.5 396.9 42.6 1.1

 9.1	  54.8	10.7	0.3
 0.4	    2.1	  0.4	0.0

The result is acceptable without testing.

4. Authors: U. Strauss, G. Altmann

5. References

Lee, Sank-Oak (1986). An explanation of syllable structure change. Korean Language Research 22, 195-213. Vennemann, T. (1982) (ed.). Zur Silbenstruktur der deutschen Standardsprache. Silben, Segmente, Akzente: 261-305. Tübingen: Narr. Zörnig, P., Altmann, G. (1993). A model for the distribution of syllable types. Glottometrika 14, 190-196.