Lexeme nets
1. Problem and history
Lexeme nets are constructed in the same way as definition chains but here all definitory concepts/lexemes (hyperonyms) are taken into account. Usually one uses monolingual dictionaries. Three examples (Fig. 1 to 3) illustrate the procedure (Hammerl 1989b):
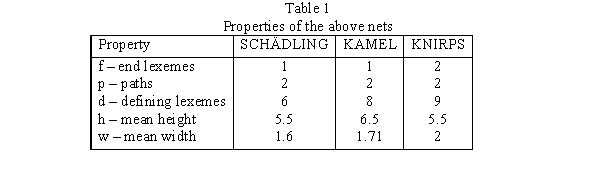
In Table 1 the properties of these nets are presented, namely
f – the number of end lexemes (concepts)
p – the number of paths from the basic lexeme to the highest (most abstract) one
d – the number of defining lexemes (i.e. all except the basic one)
h – the mean height of the net
w – the mean width of the net
The mean height h is defined as
(1)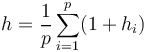
where 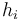 is the number of lexemes laying on path i. Thus for SCHÄDLING we have
is the number of lexemes laying on path i. Thus for SCHÄDLING we have
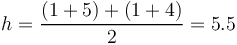 .
.
The mean width w is defined as
(2)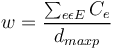
where 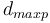 is the number of lexemes on the longest path, e.g. in SCHÄDLING the left path touches 5 lexemes
is the number of lexemes on the longest path, e.g. in SCHÄDLING the left path touches 5 lexemes
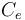 is the number of edges (e) crossed (C) by a horizontal line separating the lexemes on this path, as shown in Fig. 1
is the number of edges (e) crossed (C) by a horizontal line separating the lexemes on this path, as shown in Fig. 1
E is the set of edges (lexemes)
For Fig. 1 we have
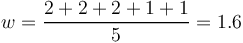 .
.
All hypotheses are due to Hammerl (1989b).
2. Hypotheses
2.1. The number of final (highest) lexemes, the number of paths and the number of defining lexemes follow the 1 displaced right truncated negative binomial distribution.
2.2. The distributions of mean height and mean width follow the continuous analog of the negative binomial distribution, i.e. the gamma distribution.
3. Derivation
3.1. End lexemes
Hammerl (1989b) uses the Zipfian synergetic argumentation: The speaker diversifies mean-ings, i.e. creates polysemy with force b whereby the number of end lexemes in nets (x) increases. The hearer counteracts with force c. All other forces are subsumed under the ceteris paribus condition designated by the constant a. Putting these condition together we obtain
(3)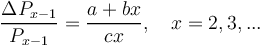
resulting in
(4)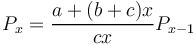 .
.
Substituting a/(b+c) = k-1, (b+c)/c = q, we obtain the well known relation
(5)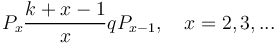
yielding
(6)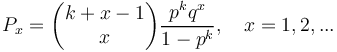
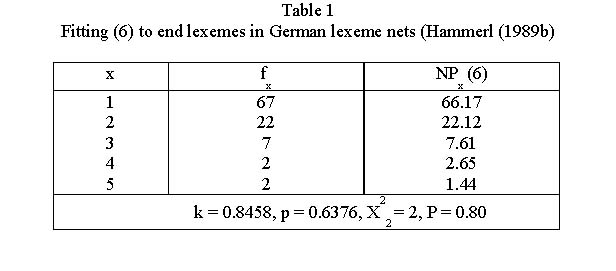
representing the distribution of end lexemes in form of the 1-displaced negative binomial distribution. In Table 1 und Fig. 4 an illustration is presented.
Example. Distribution of end lexemes in 100 German lexeme nets (Hammerl 1989b)
3.2. Number of paths
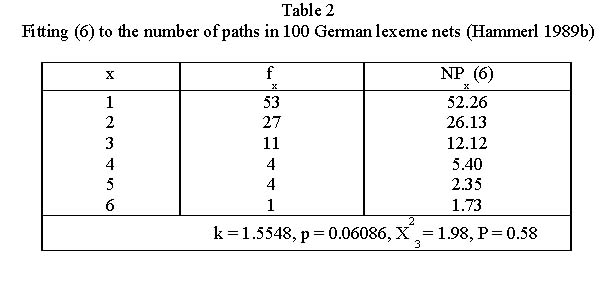
The derivation with speaker´s force b enlarging the number of paths (polysemy), c controlling this process and the ceteris paribus condition a the same result as in 3.1 follows. An example is presented in Table 2 and Fig. 5.
Example. Distrubution of the number of paths in German lexeme nets (Hammerl 1989b)
3.3. Number of lexemes in the net
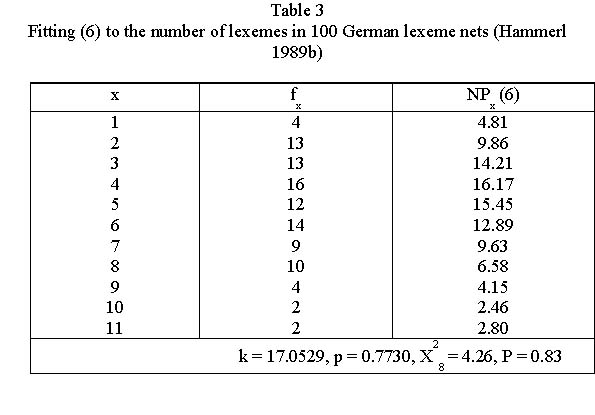
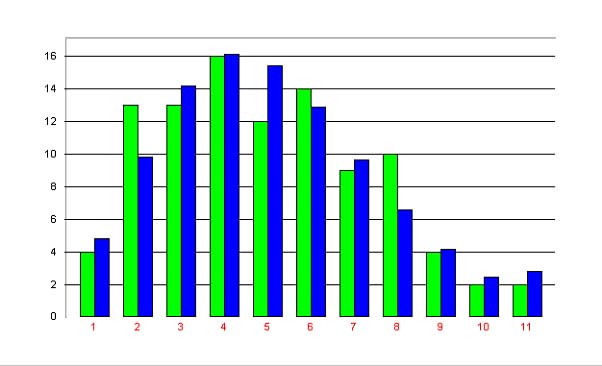
The same argumentation as above: increasing polysemy by the speaker, controlling it by the hearer and the ceteris paribus condition yield again (6). An example is shown in Table 3 and Fig. 6.
3.4. Mean width of nets
The argumentation is the same as above but with mean width we have a continuos variable. The speaker creates polysemy entailing greater width, the hearer controls it. All other forces are constant (a), thus
(7)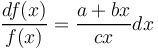
Setting a/c = A, b/c = B we obtain
(8)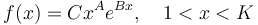
where 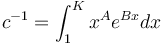 is the normalizing constant. Evidently (8) represents the doubly truncated gamma distribution. In Table 4 we present Hammerl´s example. As a matter of fact, the truncation on the right side is not necessary.
is the normalizing constant. Evidently (8) represents the doubly truncated gamma distribution. In Table 4 we present Hammerl´s example. As a matter of fact, the truncation on the right side is not necessary.
Example. Mean width of German lexeme nets (Hammerl 1989b)
3.5. Mean height of nets
Hammerl´s argumentation is slightly different but the result is identical wuth (8). The speaker tends to restrict the height of nets with force b against the force k tending to develop abstract concepts; the hearer tends to reduce the size of nets (c) but tends to enlarge the number of concept with low abstractness (m). Put together, one obtains
(9)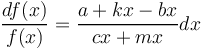
substituting k-b = r, c+m = s one obtains again (7) and integration results in (8).
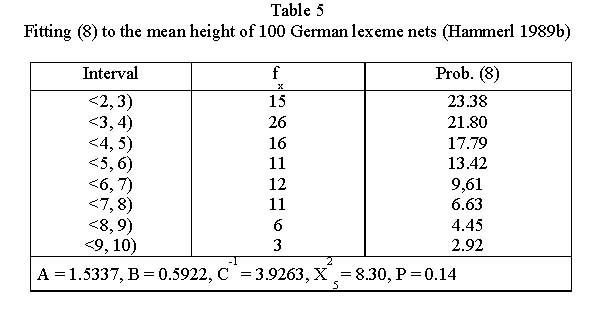
Example. Height of German lexeme nets (Hammerl 1989b)
The distribution of heights of 100 German lexeme nets is presented in Table 5.
4. Authors: U. Strauss, G. Altmann
5. References
Altmann, G., Bagheri, D., Goebl, H., Köhler, R., Prün, C. (2002). Einführung in die quantitative Lexikologie. Götingen: Peust & Gutschmidt.
Hammerl, R. (1989b). Untersuchung struktureller Eigenschaften von Begriffsnetzen. Glottometrika 10, 141-154.